この記事での学習内容 基本情報 応用情報
送信側と受信側で送受信のタイミングを合わせる信号同期制御について、代表的な方式の考え方、仕組みを理解する。
用語例: ビット同期、キャラクタ同期、フラグ同期、調歩同期、スタートビット、ストップビット、SYN同期、フレーム同期
信号同期方式
通信においては、送信側と受信側でタイミングを合わせることが必要になります。
タイミングを合わせなければ、受信側はデータの始まりと終わりを知ることも出来ません。この、通信においてタイミングを合わせることを「同期」といいます。
一般的な伝送路の同期方式は、ブロック同期方式とビット同期方式に分類されます。
ビット同期方式は電話網などで使われる同期方式です。
通常の通信では、ブロック同期方式が使われます。
ブロック同期方式の代表的なものに、調歩同期方式、キャラクタ同期方式、フレーム同期方式があります。
調歩同期方式
調歩同期方式は、文字符号の前後に同期のためのビットを付加する方式です。
1つの文字は8ビットですが、この8ビットの前に開始と終了を示す特別なビットを付加します。
開始を示すビットを「スタートビット」、終了を示すビットを「ストップビット」と呼びます。通常、スタートビットは0、ストップビットは1、データが無い場合は1を取ります。
受信側は、スタートビットとストップビットによって、文字の始まりと終わりの位置を知ることが出来ます。
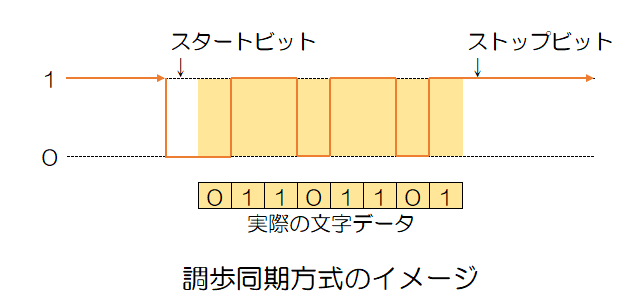
文字毎にスタートビットとストップビットが付き、伝送効率が悪いため、低速な通信で利用されます。
キャラクタ同期方式(SYN同期方式)
キャラクタ同期方式は、同期用の制御文字を使い、キャラクタ(メッセージ)単位で同期をとる方式です。同期用の制御文字は「SYN」と呼ばれるので、SYN同期方式とも呼ばれます。
キャラクタ同期方式には、制御文字の使い方が異なる複数の方式があります。
一つは、データ部分を識別するために、データの先頭と終端にそれぞれ別の制御文字を付加する方式です。
もう一つは、データ部分を識別する制御文字を使わずに、代わりに先頭に「SYN」を2個入れる方式です。
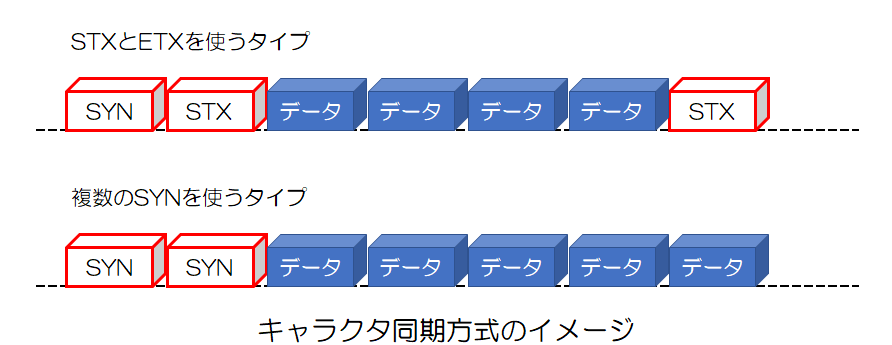
キャラクタ同期方式が利用できるのは、8ビット単位の文字情報を伝送する場合に限られます。これは不定長や8ビットではない長さのデータの場合、「SYN」と同じビットの並びが出現する可能性があるためです。
メッセージのブロックごとにビット列を付加するため、中速な通信で利用されます。
フレーム同期方式(フラグ同期方式)
フレーム同期方式は、データのブロックの区切りに特定のビットの並びを使う方式です。例えば、フレーム同期を行うある通信方式では、2進数の「01111110」という並びを使っています。
この特定のビットの並びを「フラグパターン」と呼びます。そのため、フラグ同期方式とも呼ばれます。
キャラクタ同期方式が8ビット単位の文字情報を前提としているのに対し、フラグ同期方式は任意の長さのビットデータを扱えるので、文字情報以外の画像や音声などのデータ伝送でも利用できます。
フラグ同期方式は、送信するデータが無い場合でも常にフラグを送り続けており、データが発生した際にフラグの間にデータを挿入します。
受信側はフラグ以外のビット列が現れたときに、次のフラグまでのビット列をひとまとまりのデータとしてみなします。

データのまとまり毎にフラグと呼ばれるビット列を付け加えるため、キャラクタ同期方式よりも高速な通信で利用されます。