この記事での学習内容 基本情報 応用情報
アルゴリズムは、擬似言語、流れ図、決定表(デシジョンテーブル)などを用いて表現することを理解する。また。アルゴリズムの設計方法を理解する。
用語例:再帰、分割統治法
アルゴリズム設計
アルゴリズムとは、目的にたどり着くための道筋や処理の手順のことです。アルゴリズムを考える、設計する目的は、単に問題を解く方法を見つけるだけではなく、より効率的に、より速く、より簡単に問題を解くアルゴリズムを探す事が重要です。
同じ結果を出すための処理であっても、そのアルゴリズムが異なると、処理にかかる時間や、必要となるメモリの容量などが異なってきます。効率の良いアルゴリズムほど、処理時間が短くなり、メモリの消費量が少なく済むものなのです。
アルゴリズムの表現
プログラムを設計するときには、アルゴリズムを何らかの形式で表現します。
アルゴリズムの表現には、流れ図(フローチャート)、擬似言語、決定表(デシジョンテーブル)などの表現があります。
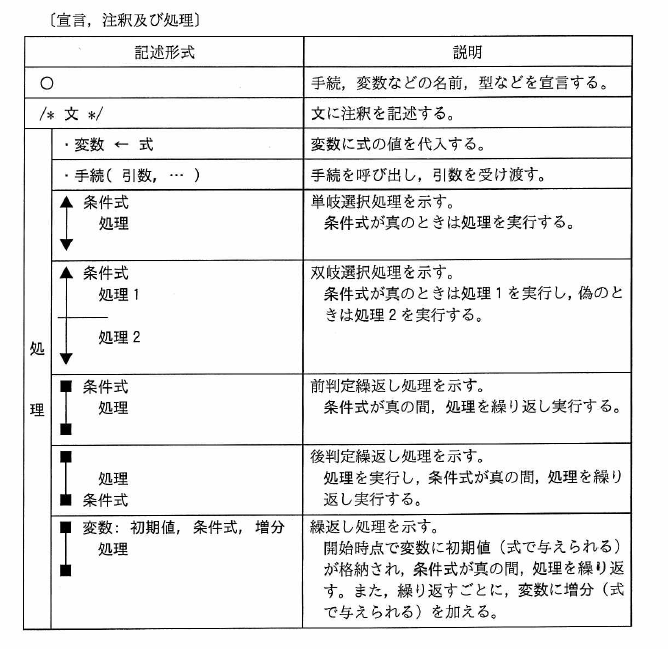
擬似言語
擬似言語は、人間が用いる自然言語とプログラム言語を混合した言語です。
アルゴリズムをできるだけ人間向きに自然言語で表現しつつ、反復や選択のように微妙な部分にプログラム言語を混用したりします。
プログラム言語と同様にテキストエディタで描くことが出来、図形を用いた表現に比べて修正が容易なのが特徴です。
テキストのみで表現した例
if a[mi] が a[i] より小なら then
a[mi] と a[i] の値を交換する
図形処理の発達に伴い、情報処理技術者試験の分野では、以下のような簡易な図記号を混用したものを擬似言語と称しています。
(実際に情報処理技術者試験で使われたものを紹介します。)
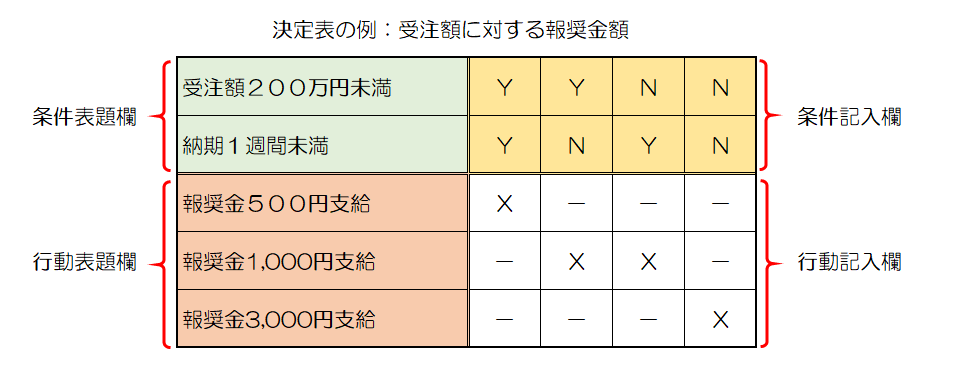
決定表(デシジョンテーブル)
決定表(デシジョンテーブル)は、条件とその条件に対する処理の関係を4つの部分からなる表にして表現する技法です。
- 条件表題欄: 問題を処理するための条件を表します。
- 行動表題欄: 条件によって取りうる行動を表します。
- 条件記入欄: 条件表題欄の各条件について、当てはまる場合は[Y]、当てはまらない場合は[N]と記載します。条件判断を必要としない場合は[-]と記載します。
- 行動記入欄: 行動表題欄の各行動について、当てはまる場合に[X]と記載します。当てはまらない場合は空欄か[-]と記載します。
大きなプログラムの場合、「行動」の単位で「サブルーチン」化することがよく行われています。(=後述:分割統治法)
また、決定表を作成するときは、取りうる条件の組み合わせを網羅し、なおかつ全てのパターンに対して、必要な処理が行われるように設計することが重要です。
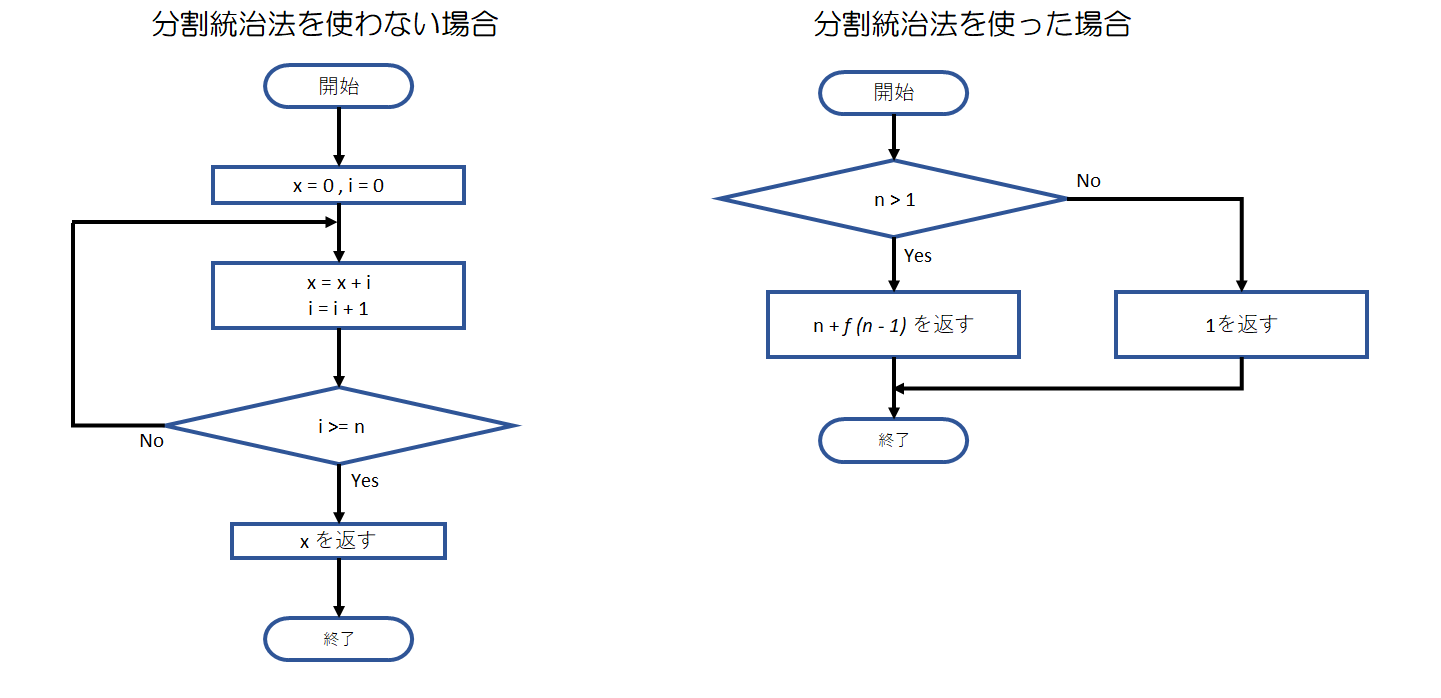
分割統治法
分割統治法とは、大きな問題を小さな問題に分割して、それぞれの問題ごとに解決に集中する方法です。
再帰のアルゴリズム、モジュール分割、オブジェクト指向設計などが分割統治法の具体的な例です。
また、ソートのアルゴリズムの中でも、マージソートやクイックソートは分割統治法に基づいて設計がなされています。
例えば、1からnまでの自然数の和を求めるアルゴリズムの場合、分割統治法を使わない場合と使った場合とでは、以下のように違った流れ図となります。