この記事での学習内容 基本情報 応用情報
グラフ理論の基本的な概念とその応用を理解する。
用語例: 無向グラフ、有向グラフ、完全グラフ、重み付きグラフ
グラフ理論
点と点を結ぶ集合であるグラフの性質についての理論をグラフ理論といいます。(ここでいうグラフは、一般的な「グラフ」とは別物)
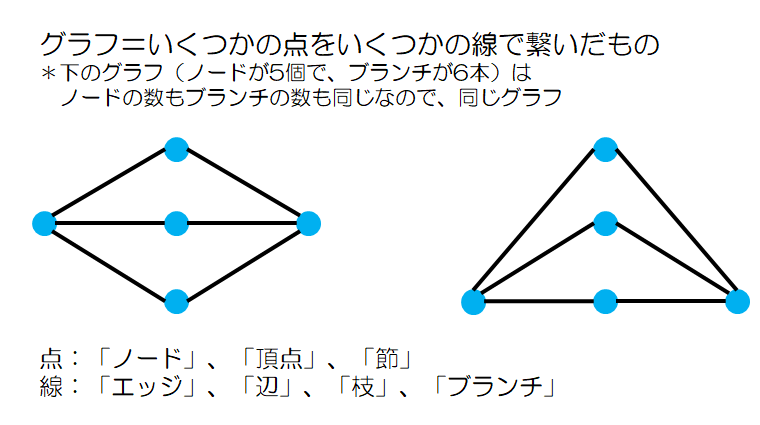
グラフとは、いくつかの接点(ノード)と呼ばれる点があり、それをある規則に基づいて結んだ線(枝:ブランチ)の集合です。
1つの接点(ノード)に付いている線(枝:ブランチ)の数を次数といいます。
現実世界の様々な要素を節点に置き換えて、その関係性を分析する際に使用されます。
鉄道の路線図などのように、節点同士の距離などに重点を置かず、節点同士のつながり方に重点が置かれます。
また、つながり方の向きを考えるグラフを「有向グラフ」、向きを考えないグラフを「無向グラフ」といいます。

グラフの次数
グラフの次数は以下のような特性を持っています。
- すべての次数の合計は必ず偶数個になる。(ループしているノードは2本として数える)
- 次数が奇数になるノードの数も必ず偶数個になる。
グラフアルゴリズム
グラフを探索するアルゴリズムで、探索の仕方によって幅優先順探索法と深さ優先順探索法があります。
幅優先順探索法
探索の優先順位を横方向にした探索法で、根から始め、左から右へ浅い方から探索します。

探索順は、節の数値が探索順となります。
深さ優先順探索法
探索の優先順位を縦方向にした探索方法です。探索の仕方によって、さらに3種類に別れます。