この記事での学習内容 ITパスポート 基本情報 応用情報
度数分布表、ヒストグラム、代表値、ばらつき、相関関係、回帰直線、分散分析、検定など統計分析の手法を理解する。
用語例:中央値(メジアン)、最頻値(モード)、平均値、標準偏差、分散、相関係数、推定、回帰分析、帰無仮説、有意水準、カイ二乗検定
統計
ある集団に関するデータを集めてその分布を調べ、数値化して集計することを統計といいます。
統計を取り、様々な分析手法(表やグラフを活用する)を用いると、その集団の性質や特徴をつかむことが出来ます。
度数分布表
度数分布表は統計の基礎資料となるものです。
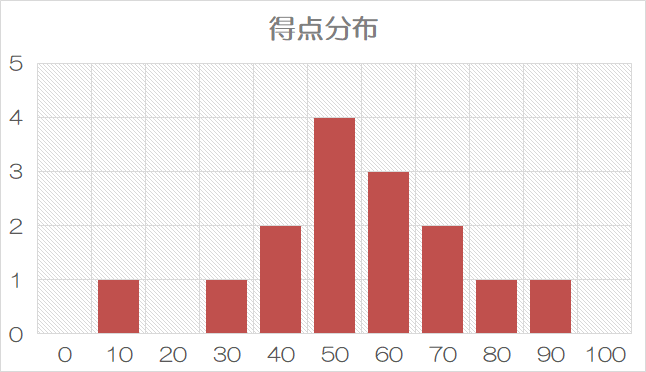
例えば、15人が受けた試験の得点を10点刻みで採点し、結果を次のようにまとめたとします。

上の表のように、データ全体の発生範囲をいくつかの階級に分け、それぞれの階級にデータがいくつ分布しているかを示す表のことを、度数分布表といいます。
ヒストグラム
ヒストグラムはデータ分布の状況を見るために作られる図解です。
度数分布表を棒グラフにしたもので、連続した数値を区分ごとに分けて、横軸の目盛とします。
ヒストグラムにおいて、それぞれの範囲に属するデータの件数を「度数」といいます。ある区分に集中してデータが分布する場合、その区分を中心とした山形のグラフになります。
正規分布
正規分布は、データが平均値を中心として+ーに対象に分布した状態のことです。
一般的に、ある事象について一定数以上のデータを抽出して統計と取ると正規分布になり、そのヒストグラムは左右対称の釣鐘型になると言われています。
ポアソン分布
ポアソン分布は、発生確率の低い事象で見られる確率分布です。
例えば、電話における単位時間中の着呼数、工場における不良品の発生数などがポアソン分布に従うと言われています。
単位時間中に平均でλ 回発生する事象が、ちょうど k 回(k は0を含む自然数)発生する確率をグラフに取ると、λ = k となる時にピークが来るようなグラフになる。
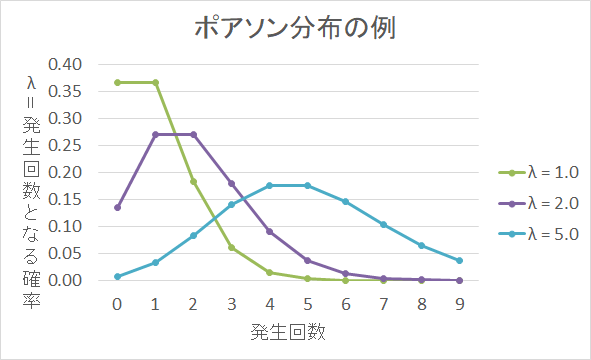
例:1時間に5人の利用者があるATMで、実際に1時間にATMを利用した人数の分布。
指数分布
指数分布は発生階数の低い事象で見られる確率分布です。指数分布は信頼度の計算などでよく使われます。(信頼度:機械の部品が故障しない確率)
指数分布はポアソン分布と関係していて、電話における単位時間内の着呼数がポアソン分布の時、着呼間隔は指数分布になります。
単位時間中に平均でλ 回発生する事象が、「次に発生するまでの時間」の分布。

例:1時間に5人の利用者があるATMで、次にATMを利用する人が来るまでの時間の分布。
カイ二乗分布
独立に標準正規分布に従う k 個の確率変数 X1, …, Xk をとる。 このとき、統計量 の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。この分布は自由度 k に応じて下図のような形をとる。
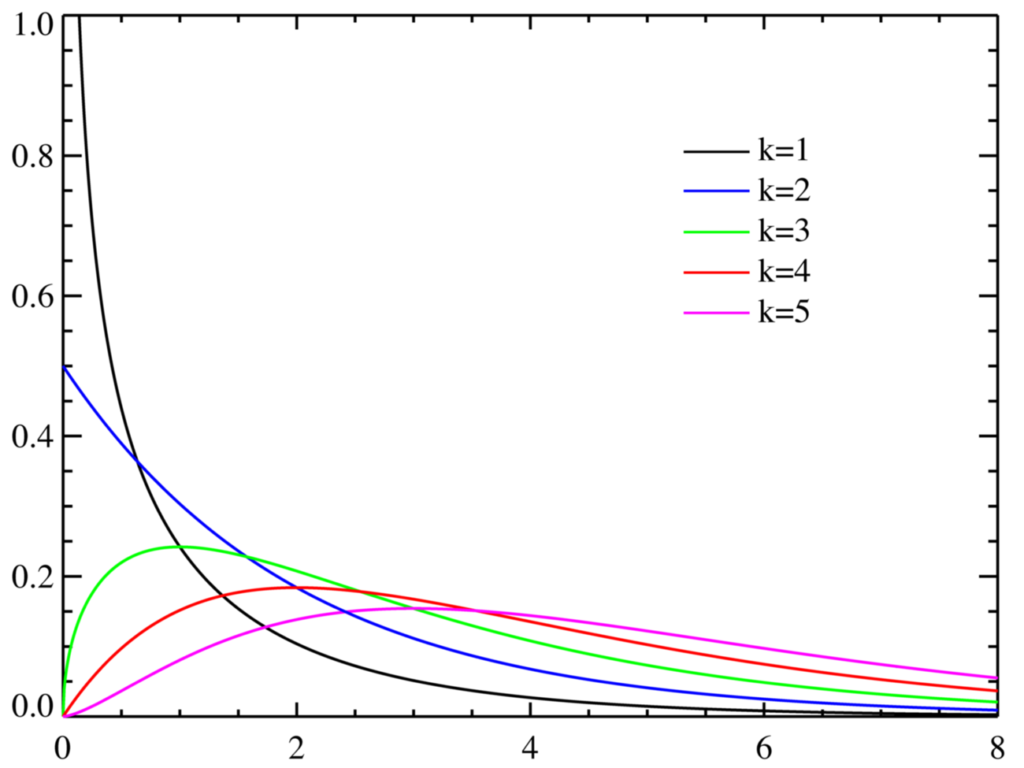
実際に様々な観測データを取得した場合、その分布には誤差が含まれるため、理論的に求められる分布と完全には一致しない。例えば、サイコロの各目の出る確率は1/6であるが、だからといってサイコロを6回振ったら各目が1回ずつ出るわけではない。振る回数を多くすればおおよそ1/6ずつに近い分布になると思われるが、均等に1/6ずつにはならない。
こういった時に「実際の観測データが理論値の分布にほぼ等しいとみなせるかどうか」を分析する際に、カイ二乗分布が用いられる。(この分析方法のことを「カイ二乗検定」とよぶ)
統計の指標
統計の指標として、平均、メジアン、モード、レンジなどの値がよく用いられます。これらの値のことを「代表値」といいます。
代表値とは、多数あるデータの値を一つの数値で代表させた値です。
| 平均 | データの合計値をデータの個数で割った値 |
| メジアン | 中央値。データを大小順に並べた時に中央の位置に来る値 |
| モード | 最頻値。データ中に存在する個数が最も多い値 |
| レンジ | 範囲。データの最大値と最小値の差 |
以下の度数分布表があった場合、各代表値は以下のようにして求めます。

平均
データの合計値:10+30+40×2+50×4+60×3+70×2+80+90 = 810
データの個数:15
平均:810 ÷ 15 = 54
メジアン
中央に来る値は8番目の値なので、メジアンは50。
なお、集計データが偶数個のときはメジアンは2つの中央値の平均を使う。
例:10, 30, 40, 50, 70, 80 の6つのデータのメジアン
3番めと4番目が2つの中央値になるので、(40+50) ÷ 2 =45
モード
得点の中で出現度数が最も高い値は50 (4回) なので、モードは50
なお、最頻値が複数ある場合はそれら全てがモードとなる。
レンジ
得点の最大値:90
得点の最小値:10
レンジ: 90 – 10 = 80
散布度(ばらつきの度合い)
データの分布の特性は代表値だけでは表しきれません。
例えば、以下のようなケースで代表値として平均値を採用する場合、下記の2つのケースはどちらも平均値は10で変わりません。
- ケースA:0,10,20
- ケースB:5,10,15
しかし、データのばらつき度合いが異なります。このばらつきの度合いを示すのが散布度です。
代表的な散布度には分散と標準偏差があります。
分散は以下の式で求めます。
Σ( データの値ー平均値 )2
これに基づいて、先ほどの2つのケースの分散を求めます。
- ケースA:0,10,20
( 0 – 10 )2 + ( 10 – 10 )2 +( 20-10 )2 =100 + 0 + 100=200 - ケースB:5,10,15
( 5 – 10 )2 + ( 10 – 10 )2 +( 15-10 )2 =25 + 0 + 25=50
標準偏差
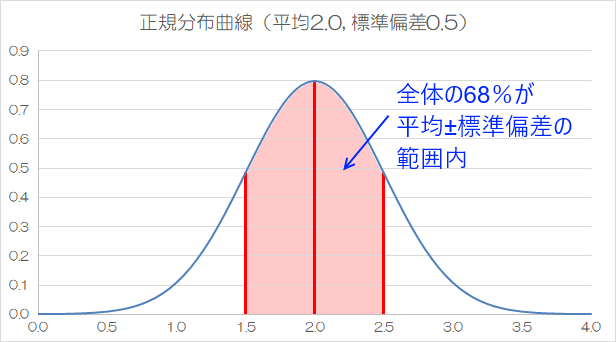
正規分布の形は、母集団の平均値と、母集団の分散から求めた標準偏差で決まります。
分散とはデータのばらつきを表す値で、標準偏差は分散のルート(√ )です。
平均をμ (ミュー)、標準偏差をσ (シグマ) と表すと、正規分布では約68%のデータが μ ± σ の範囲に収まり、約95%のデータが μ ± 2σ の範囲に収まります。
回帰直線
散布図(*1)のデータに、できるだけ一致する曲線を求める分析を「直線回帰分析」と呼びます。
直線回帰分析では、最小二乗法と呼ばれる方法が、一般的には使われます。
これは、実際のデータの値と、直線上の値の差の二乗が最小になる直線を求める分析方法です。直線は「傾き(*2)」と「y切片(*3)」と呼ばれる2つの値で定まります。
回帰直線は、実際のデータとは一致しません。データの分布によっては回帰直線と一致する度合いが大きかったり小さかったりします。
データの分布が回帰直線と一致する度合いを「相関」といいます。回帰直線に一致するほど「相関が強い」といいます。
相関の強さを数値で示したものが「相関係数」です。相関係数は-1~1までの値を取ります。
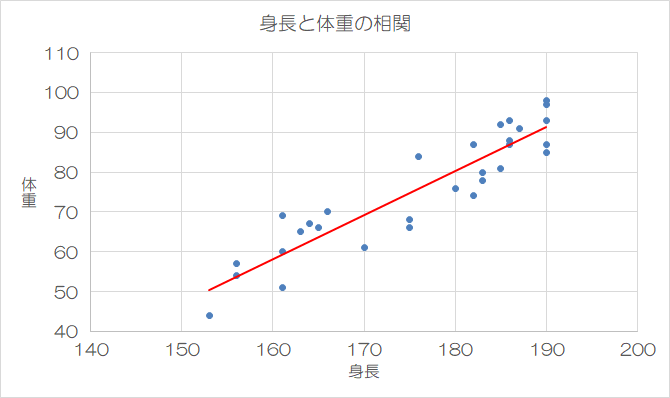
(*1)散布図:2つの属性値の相関関係を表したグラフ(例:身長と体重の相関など)
(*2)傾き:xが1増加した時のyの変化量を表す値。傾きがプラスの場合は右上がりの直線、マイナスのときは右下がりの直線となる。絶対値が大きいほど傾きは急。
(*3)y切片:直線とy軸の交点でのyの値。y切片が大きいほど、直線はグラフの上方に位置する。
標本調査
調査対象の件数が多い場合、対象全てを調査することが難しい場合があります。
このような場合には、調査対象の中から一部を取り出して調査を行い、全体を推定します。
このような分析を標本調査と呼びます。
例)テレビ視聴率、世論調査など
 の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。この分布は自由度 k に応じて下図のような形をとる。
の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。この分布は自由度 k に応じて下図のような形をとる。