この記事での学習内容 基本情報 応用情報
連立一次方程式の解法など、数値計算に関する基本的な内容を理解する。
用語例:行列、対数、掃出法、近似解法、収束、誤差
単項式、多項式、次数
単項式は、数値や文字の「掛け算」だけで造られた式のことです。2x や 3b などは単項式です。
多項式は単項式の足し算、引き算の形式で造られた式です。3x-2b と言った式が多項式の例です。多項式の中にある単項式は多項式の「項」と呼びます。
次数は、単項式の場合掛け算されている「文字の個数」です。3xy という式の場合、掛け算されている文字はx,y なので次数は2、x3 の次数は3となります。
多項式の場合は、一番次数の高い項の次数がその式の字数です。
x2+y という式の場合、x2 の次数2が一番高いので、この式の次数は2となります。
方程式、1次方程式
方程式とは、x , y といった「未知数」を含む等式のことです。未知数は「まだ分かっていない数」のことで、xやy といった文字で表します。
一次式とは、未知数の2乗以上を含まない式のことです。一元一次式は未知数が1つの一次式、二元一次式は未知数が2つの一次式です。
1次方程式とは、未知数の2乗以上の関係を含まない等式のことです。
連立一次方程式
連立方程式とは、同時に成立する複数の方程式です。方程式を組み合わせることにより、複数の未知数の解を求めることが出来ます。
連立方程式の名称は、未知数の数と次数によって決まります。
未知数の数が2個ならば2元連立方程式、3個ならば3元連立方程式となります。
つまり、連立一次方程式とは、複数の未知数を含む複数の1次方程式です。
連立一次方程式の解法
「連立一次方程式を解く」とは、与えられた方程式を全て同時に成立させる未知数の値を求めることです。数学の問題を解く方法のことを「解法」といいます。
連立方程式の解法には、加減法、代入法、等置法などがあります。連立一次方程式はこうした解法を用いて式を1元1次方程式の形にしていき、複数ある未知数を一つ一つ順番に確定していきます。
行列
行列とは、数学用語では、数値や変数を長方形に並べたものという意味になります。行列では横の並びを行、縦の並びを列と呼びます。下図の a , b , c , d などを行列の要素、あるいは成分といいます。
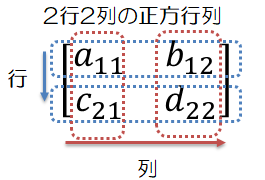
行列の要素を数値などで具体的に記述せずに、一般化して文字で表す場合、要素の右側に要素の位置を示す「添え字」を付けます。
上の図の「b12」であれば、最初の1は行番号、つぎの2が列番号を表します。
なお、行列の中で行数と列数が等しいものを「正方行列」といいます。
行列の和
行列同士の和は、各行列の同じ添字の要素同士を足し算します。
*下図では数値の右下に添え字を付けていますが、計算の説明のために例外的につけています。
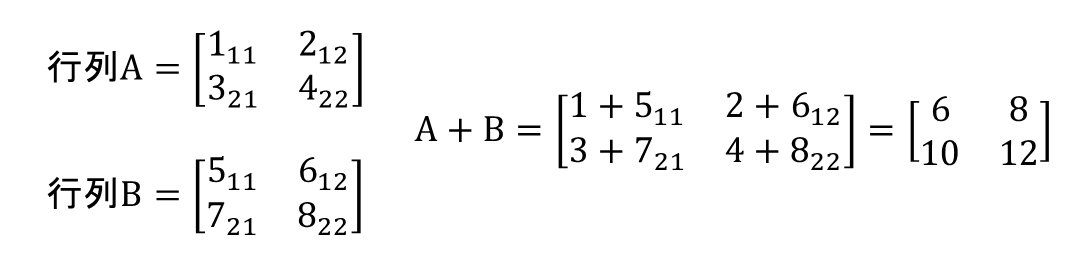
行列の差
行列の積
行列の積は、行方向と列方向を掛けたものを足して要素とします。行列の要素が1以外の場合、行列A×行列Bと行列B×行列Aの計算結果は異なります。
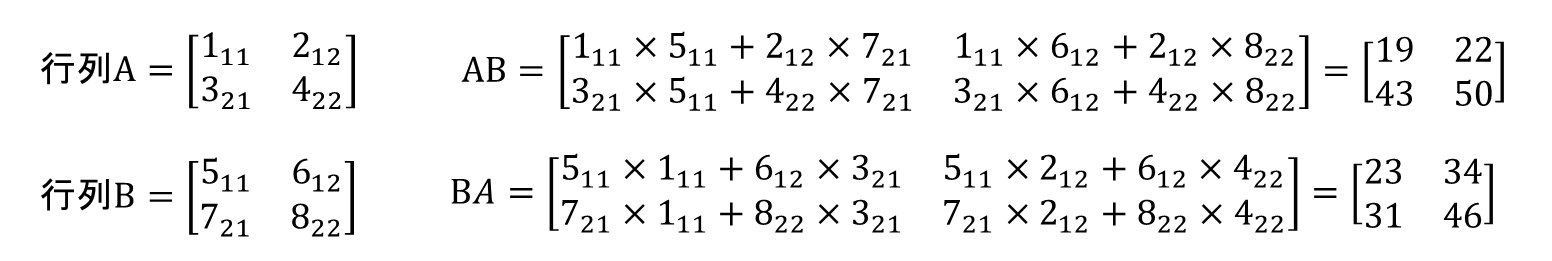
また、行列の積を「行列A×行列B」で求める場合、下図のように行列Aの列数と行列Bの行数が一致している必要があります。

例えば、行列Aが3行2列の行列だった場合、行列Bは2行n列でないと、積を求めることは出来ません。
行列による連立方程式の表記
対数
対数とは、ある数x は、ある数y を何回か掛け合わせた値であるとすると、そのかけ合わせた回数のことを言います。
数式で表すと、x = ya の a を「y を底とするx の対数」といい、 a = logy(x) と表します。
例)8 = 23 なので、log28 = 3
特に底を10とした対数のことを常用対数とよんでいます。
対数グラフ
通常のグラフでは、1, 2, 3, …と言うように、横軸も縦軸も順番に数が増えていきます。このようなグラフは少しずつ変化する値を描く場合などには有効です。
これに対して、2倍、4倍、8倍…と倍々で変化する値を描く場合などはすぐに縦軸が大きな値になって描けなくなってしまいます。
そこで、縦軸だけ対数を使うと、縦の変化量を抑えることが出来ます。このような、片側を対数としたグラフのことを「片対数グラフ」といいます。(両方対数としたグラフは「両対数グラフ」)
素因数分解
素数とは、1とその数自身以外に正の約数がない、1より大きな自然数です。
100以下の素数は、2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 の25個です。
素因数分解とは、ある正の整数を十数の掛け算の形に分解することです。
例) 78 = 2 × 3 × 13
素因数分解にまつわる法則として、「2つの異なる素数p, q の積である、ある合成数Nが与えられた時、合成数N飲みから、元の素因数p, q を求めることは非常に困難」というものがあります。
この法則を利用し、安全性の根拠としている暗号化技術として、RSAという方式があります。