この記事での学習内容 ITパスポート 基本情報 応用情報
論理式の表現,論理演算,ド・モルガンの法則などの基本法則,真理値表,カルノー図の 手法を理解する。
用語例: 否定,論理和,論理積,排他的論理和,否定論理和,否定論理積,論理関数,分 配則
論理演算
命題の真偽によって演算結果を表すことを論理演算といいます。
基本となるものに「否定(NOT)」「論理積(AND)」「論理和(OR)」があります。
| 演算 | 意 味 | 式 |
|---|---|---|
| 否定 | 1つの命題が「~ではない」と逆になる(NOT) | |
| 論理積 | 2つの命題が「~かつ~」の関係(AND) | |
| 論理和 | 2つの命題が「~または~」の関係(OR) |
論理演算はコンピュータと縁の深いモデル化の技法です。
AND、OR、NOTで複数の命題を組み合わせれば、どんな複雑な論理回路も作ることが出来ます。
また、データ間の関係も論理式に置き換えると整理できるので、プログラミングやデータベースの構築に欠かせない理論です。
否定(NOT) 、論理積(AND)、論理和(OR)
集合の論理演算は、リレーもしくは半導体回路を使った電子回路で実現することが出来ます。
真理値表のAとBを入力に見立てて、その真、偽の状態によって論理和の真理値表と同じ結果を出力する回路をOR回路、論理積と同じ結果を出力するものをAND回路、入力の否定を出力するものをNOT回路といいます。
| MIL記号 | ベン図 | 真理値表 | |
|---|---|---|---|
| Aの否定 |  | 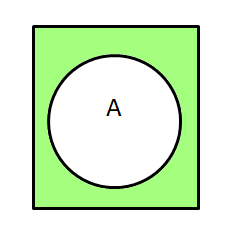 | 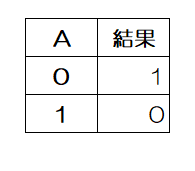 |
| AとBの論理積 | 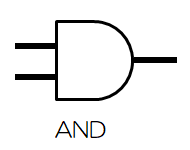 | 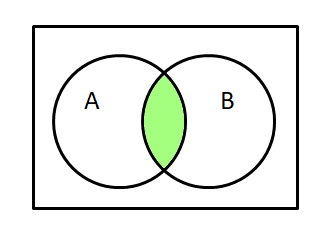 | 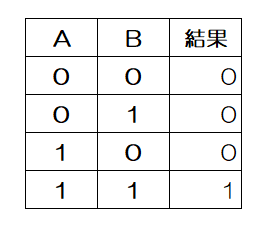 |
| AとBの論理和 |  | 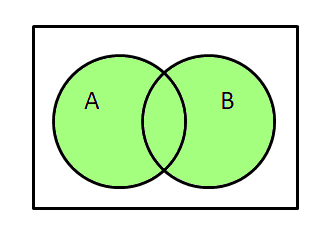 | 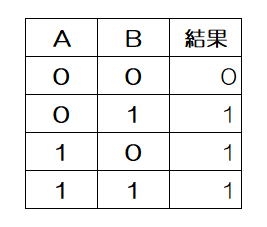 |
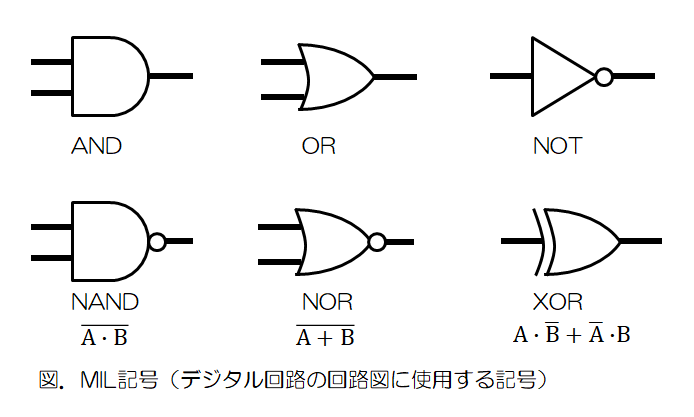
それぞれの回路は回路図上で以下の図のような記号(MIL記号)を使って表します。
NAND回路とNOR回路は、それぞれAND回路、OR回路にNOT回路を繋いだものとなります。
これらの回路を組み合わせることで、非常に複雑な論理式や機能を電子回路で実現することが出来ます。実際、コンピュータ内部で足し算やシフト演算を行うALU、命令デコーダ、タイミング制御回路、レジスタやメモリ(DRAMを除く)なども全て論理回路で構成されています。
また、基本となる論理演算を組み合わせたものもよく利用されます。代表的なものは、「否定論理和(NOR)」「否定論理積(NAND)」「排他的論理和(XOR)」です。
論理演算の一般的な法則
2つの命題を使った論理演算には、幾つかの法則が成り立ちます。
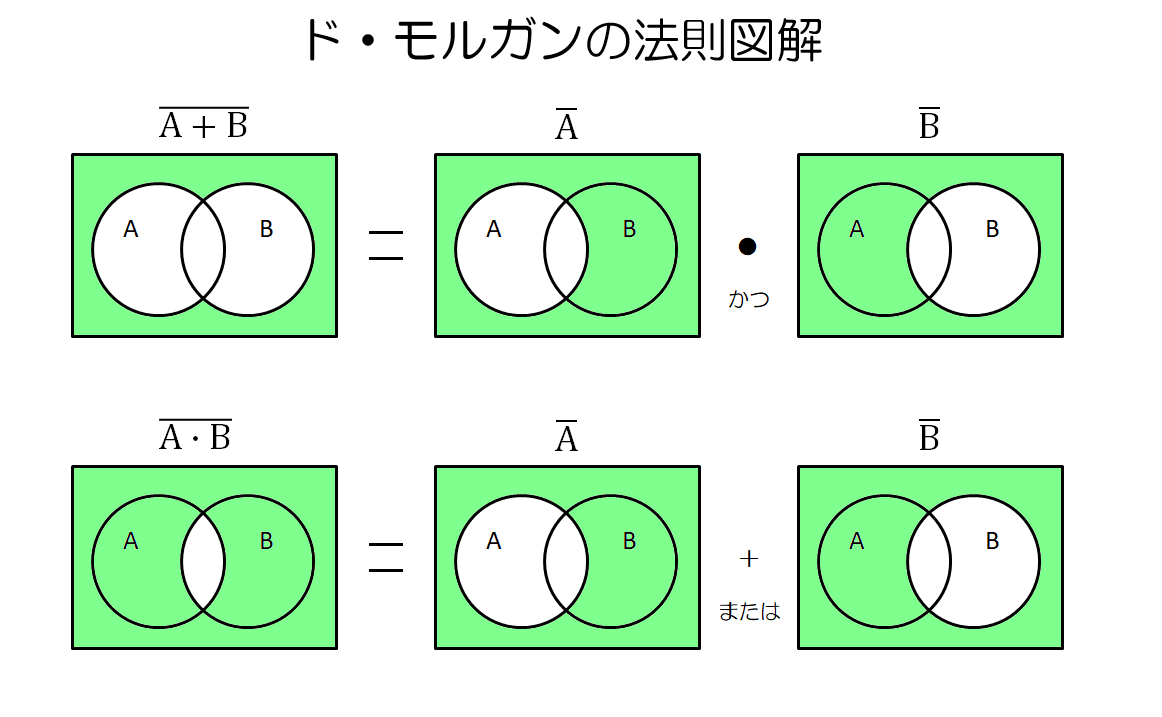
ド・モルガンの法則を始めとする、論理演算の各種の法則は、複雑な論理式を簡略化したり、別の式に変換したりする時に利用できます。
これは、プログラムの開発において、判定条件が複雑になった時、評価する式を簡略化したり、デジタル回路を設計する時に、同じロジックの回路を少ない部品点数で設計し直したり、と言った場面で役立ちます。
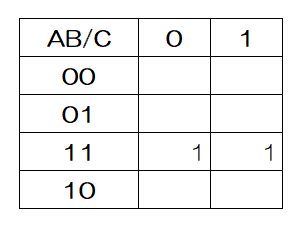
カルノー図法
カルノー図法は真理値表でパターン数が増えて見づらいときなど、論理式を簡略化するための図法。下記のような変数が3つ以上の式で、論理積の項を論理和した形(積和形)の場合に使いやすいとされている。
![]()