この記事での学習内容 ITパスポート 基本情報 応用情報
小数の表現を理解する。
用語例: 固定小数点数,単精度浮動小数点数,倍精度浮動小数点数,仮数,指数
小数の表現方法の種類
小数の表現方法には固定小数点数と浮動小数点数があります。また、浮動小数点数には、単精度浮動小数点数と倍精度浮動小数点数などがあります。
固定小数点数
コンピュータで負の数を含む整数の数値データを扱うときは、固定小数点数という方式を使うのが一般的です。
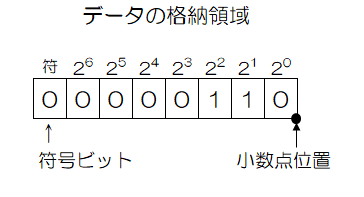
固定小数点数では、次のようにデータを記憶します。
- データの格納に必要なビット長の記憶領域をあらかじめ用意する。
- 小数点の位置を決めて、各桁の2進数値を各ビットに当てはめる。
- 先頭の1ビットを正負の符号ビットとして扱う。
なお、固定小数点数のビット長はコンピュータによって異なりますが、16ビットや32ビット長などが一般的です。
浮動小数点数
浮動小数点数は、文字通り小数点の位置が浮いて移動するように見えるので、浮動小数点数と呼ばれています。
この方式では、非常に大きな数や小さい数を扱うことが出来ます。
例えば、32ビットの固定小数点数の場合、正の数なら 231-1 が最大の数となりますが、32ビットの浮動小数点数の場合、3.4 × 1038 という非常に大きな値となります。
浮動小数点数の正規化
浮動小数点数では、同じ数値を仮数部、指数部の調整次第でいろいろな表現が可能になります。しかし、コンピュータにとって表現方法が一定ではないのは都合が悪いため、仮数部の小数第1位に0以外が来るようにします。このことを正規化とよんでいます。
なお、仮数部の整数部が基数1桁に収まるようにすることを正規化とする場合もあります。後述する「バイアス表現」を使う場合に、この方法を使います。
例) 1.5 という10進数の値を浮動小数点数として表現
15 × 10-1
1.5 × 100 ← こちらを正規化されたデータとする場合もある
0.15 × 101 ← 正規化されたデータ
0.015 × 102
浮動小数点数の表現方法
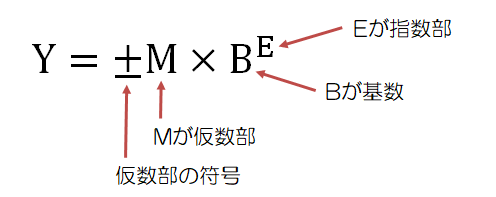
浮動小数点数は、仮数部の符号、指数部、仮数部を用いて表現します。
仮数部の符号は、0か正の数の場合は0を、負の数の場合は1とします。
指数部は基数を何乗するのかという値を入れます。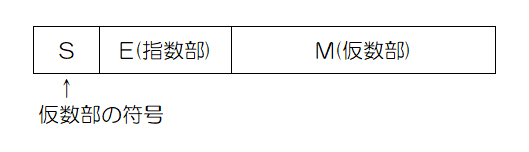
浮動小数点数の表現形式
浮動小数点数の表現形式にはいくつかの種類があります。
ここでは、24ビットの浮動小数点数について、『バイアス表現』と使わない形式と使う形式を紹介します。
*バイアス:下駄履き、底上げ
バイアス表現を使わない形式
24ビットの内、1ビットを符号ビット、7ビットを指数部、16ビットを仮数部とします。
これを用いて、10.375(10) を表現してみます。
10.375(10) を2進数で表すと、1010.011(2) となります。この数は正の数ですので、符号ビットは「0」となります。
次に、仮数部が1未満になるように正規化を行います。
1010.011 = 0.1010011 × 24 となるので、仮数部の上位から「1010011」を入れ、残りビットは0とします。
最後に指数部は4を7桁の2進数に変換し、「0000100」を入れます。
バイアス表現を使う形式
24ビットの内、1ビットを符号ビット、8ビットを指数部、15ビットを仮数部とします。
これを用いて、-10.375(10) を表現してみます。
-10.375(10) を2進数で表すと、-1010.011(2) となります。この数は負の数ですので、符号ビットは「1」となります。
次に、仮数部が1.**になるように正規化を行います。
1010.011 = 1.010011 × 23 となるので、ここから小数点以下の部分「010011」を抜き出し、仮数部の上位から「010011」を入れ、残りビットは0とします。
最後に指数部分ですが、ここで『バイアス表現』を使います。
バイアスとは「下駄を履かせる、底上げする」という意味ですが、マイナスの数値を符号なしの2進数で表すために、所定の数(=バイアス値)を加えて表す方法です。
今回は指数部分を8ビットとし、最小値の-127を0と表すために、バイアス値を127とします。指数部の値は3ですので、これに127を加えた130を2進数に変換し「10000010」を指数部に入れます。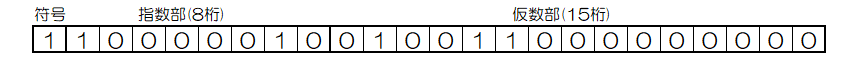
単精度浮動小数点数と倍精度浮動小数点数
浮動小数点数を32ビットで表現する方法を単精度浮動小数点数といいます。
ここから使用する桁数を増やし、精度を上げる場合は64ビットの倍精度浮動小数点数を利用します。