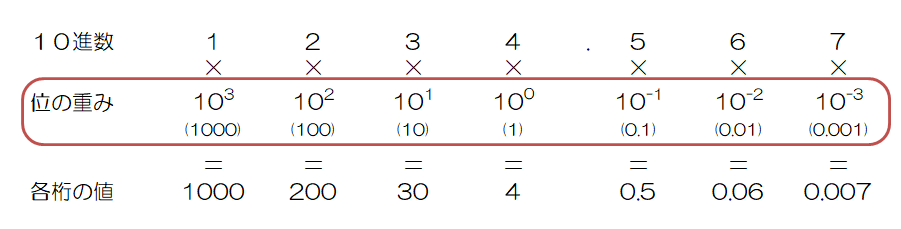この記事での学習内容 ITパスポート 基本情報 応用情報
2 進数,8 進数,10 進数,16 進数,n 進数の表現,2 進数と 10 進数などの基数の変換手法 を理解する。
記数法
私たちが一般的に数値を扱うときには0~9までの数字を使う、「10進法」を用いています。
一方で通信やコンピュータの分野では「2進法」「8進法」「16進法」などが使われます。
10進法では0~9までの数字を使い、「10」を桁上りの基準としていますが、2進数では「2」、16進数では「16」が桁上りの基準としています。
この桁上りの基準をどの値にするか、0からどの数字(文字)までを使って数を表すかを決めたものを「記数法」といいます。
一般的には、桁上りの基準の値を用いて「n進法:nを基準に桁上りする」となっています。
| 桁上りの基準 | 使う数字・文字 | 表記方法の例 (10進数の100の場合) |
|
|---|---|---|---|
| 2進法 | 2 | 0と1のみ | 0b1100100 1100100(2) |
| 8進法 | 8 | 0~7の数字 | 0144 144(8) |
| 10進法 | 10 | 0~9の数字 | 100 |
| 16進法 | 16 | 0~9までの数字と英字のA, B, C, D, E, F | 0x64 64(16) |
基数と重みーn進数の表現
10進数の「1000」という値は「1 × 103」と表すことも出来ます。
この時の1を「仮数」、10を「基数」、103を「重み」といい、10進数の各桁はこの表現による値となっています。
言い換えれば、「基数」は桁上りの基準で、「仮数」は実際に表示されている数字、「重み」はどの桁かを表す値となります。
(但し、重みの桁数は0が1の位となる点に注意)
このように、nを基数として数値を表す記数法を「n進数」といいます。
なお、n進数で小数を表すときには、「n-1」「n-2」といった重みを使います。
・n0 = 1 (nの「0乗」は必ず1になる。)
・n-x = 1 / nx
これらを踏まえて、「1234.567」という10進数の数値を基数と重みを使った表現で表すと下の式および図のようになります。
1234.567 = 1000 + 200 + 30 + 4 + 0.5 + 0.06 + 0.007
= 1 × 103 + 2 × 102 + 3 × 101 + 4 × 100 + 5 × 10-1 + 6 × 10-2 + 7 × 10-3
基数と重みー2進数の場合
2進数は2を基数とする数え方です。2を基準に桁上りするので、数の表記には0と1のみを使います。
例えば2進数の「1010」という値を重みを使った表現で表すと以下のようになります。
1010 = 1 × 23 + 0 × 22 + 1 × 21 + 0 × 20
2進数の加算と減算
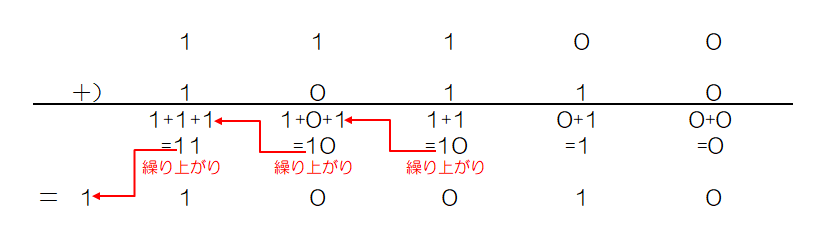
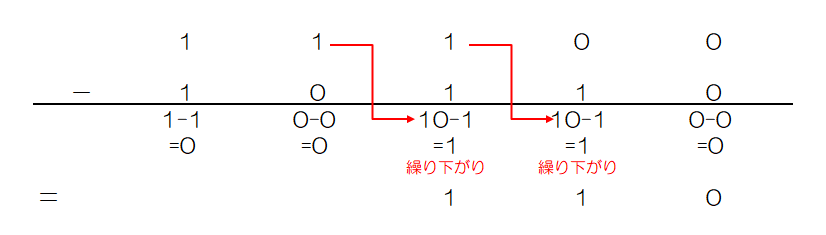
2進数同士の加算、減算は10進数の時と同様、筆算で解くことが出来ます。
例1) 11100(2) + 10110(2)
例2) 11100(2) - 10110(2)
基数変換
また、10進数と2進数など、n進数同士は互いに変換することが出来ますが、この変換のことを「基数変換」といいます。
10進数と2進数の変換
2進数を10進数に変換
2進数を10進数に変換するには、各桁の数に重み(2のべき乗)を掛けて合計します。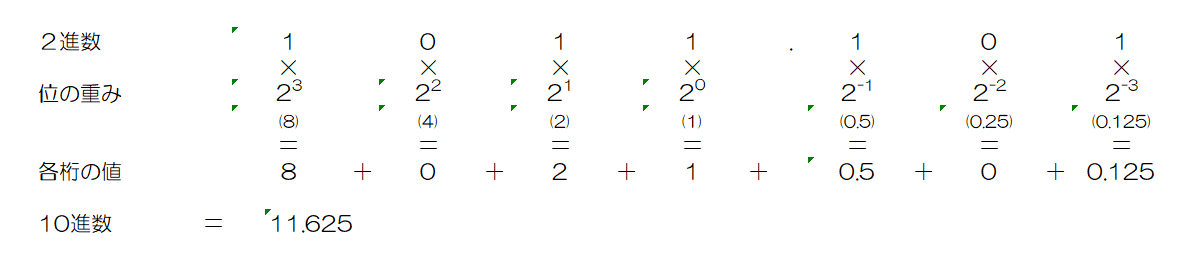
10進数を2進数に変換(整数部分)
10進数の整数を2進数に変換するには、10進数を商が0になるまで2で割り続け、余りを拾い出して順に並べると2進数になる。
*拾い出して並べる順は図を参照。
10進数を2進数に変換(小数部分)
10進数の小数を2進数に変換するには、10進数を2倍し、1の位を取り出す、という作業を小数部分がなくなるまで繰り返す。
*拾い出して並べる順は図を参照。
8進数と16進数
コンピュータ内部では情報は2進数で扱われているので、そのまま表記したいところですが、少し大きな値になると桁数が非常に多くなってしまい、ただでさえ分かりにくい2進数がさらに分かりにくくなります。
そこで桁数を少なくするためのテクニックとして、8進数や16進数を用います。
8進数の1桁は、2進数の3桁に対応し、16進数の1桁は2進数の4桁に対応するため、2進数から8進数・16進数には簡単に置き換えることが出来るためです。
2進数と8進数・16進数を変換するには、以下の表で対応を覚えてしまいましょう。
| 10進数 | 2進数 | 8進数 | 16進数 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
2進数と8進数の変換
2進数の3桁は、8進数の1桁に対応しています。
これを利用し、小数点を基準に3桁ずつ区切り、それぞれを8進数に変換していくと8進数の値となります。
*3桁に足りない部分は0を補います。整数部の場合は左に、小数部の場合は右に補います。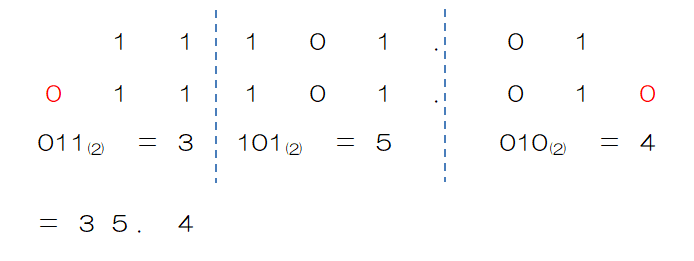
2進数と16進数の変換
2進数の4桁は、16進数の1桁に対応しています。
これを利用し、小数点を基準に4桁ずつ区切り、それぞれを16進数に変換していくと16進数の値となります。
*4桁に足りない部分は0を補います。整数部の場合は左に、小数部の場合は右に補います。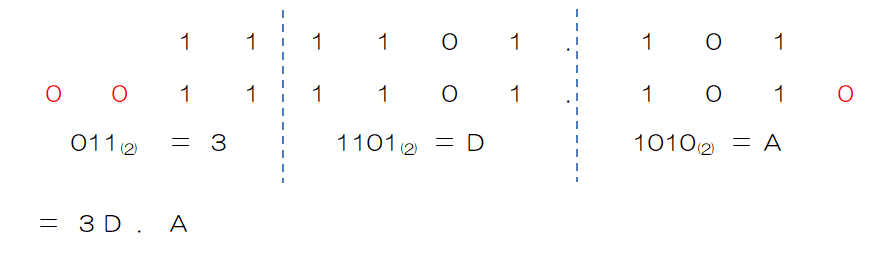
情報を表す単位
コンピュータ内部では、電流のON/OFFによって情報を表現しています。
この電流のON/OFFを数字に置き換えた場合、0と1の2つの数字のみを使う2進数のほうが都合が良いため、コンピュータ内部でデータを処理する場合には2進数が用いられています。
ビット
コンピュータはデータ処理に2進数を用いますが、この2進数1桁分の情報(ON/OFF、0 or 1)がコンピュータで扱うデータの最小単位で、「ビット(bit)」といいます。
1ビットの情報量で表せるデータの範囲は、2進数1桁分ですので、0か1の2パターンです。
ビットで表すことの出来る範囲
1ビット(=2進数1桁)で表すことの出来る情報は0か1の2通りです。
これを2桁分使うと、「00」「01」「10」「11」の4通りが表せます。
2=21、4=22ですので、nビット(2進数n桁)では、2n通りの情報を表すことが出来ます。
バイト
データの最小単位はビットですが、記憶装置の保存容量などを表す単位として「バイト(byte)」という単位もよく使われます。
「1バイト = 8ビット」として換算しますので、1バイトで表すことの出来る範囲は28で256通りとなります。