この記事での学習内容 ITパスポート 基本情報 応用情報

探索、併合のアルゴリズムを理解する。
再帰的アルゴリズムの考え方、特徴、実現に適したデータ構造を理解する。

用語例：線形探索法、二分探索法、ハッシュ表探索法、シノニム対策

探索

「探索」とは配列などに格納されたデータの集まりから、特定のデータを探すことです。その値が見つかる場合と、見つからない場合があり、複数ある場合には最初の一つを見つければ良い場合と、全てを見つける必要がある場合があります。

つまり、探索の結果も見つかったかどうかだけではなく、何番目に見つかったか、いくつあったか、という情報を帰す場合があります。

線形探索法（リニアサーチ）

線形探索法とは、配列の先頭から１つずつ調べてゆき、求めるデータが見つかるか、又は配列の最後まで探し終わったとき探索を終了する方法です。

以下に、線形探索法の場合の流れ図を示します。ここでは、４つの数が入った配列の中から、「５」を探すものとします。

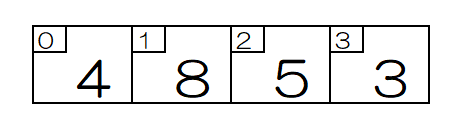
探索する数「５」を変数 x とし、探索対象の数を n [ i ] と表します。
先頭の n [ i ] から順に x と比較していき、同じものが見つかったら、その添字 i を表示して探索を終了、最後まで探して見つからなかった場合は、「無し」と表示して終了します。

なお、線形探索法を行なった場合の探索回数は以下の通りとなり、オーダ記号で表すと O(n) となります。（データは n 個とする）

• 最小探索回数：　１回
• 最大探索回数：　ｎ回
• 平均探索回数：　（ｎ＋１）÷２回

番兵を使った線形探索法

線形探索をより簡単にするために、配列の最後に「番兵」と呼ばれるデータを追加する方法があります。

探すデータと同じ値を、配列の最後尾の次に追加しておくことで、反復の終了条件として、添字の範囲を毎回チェックする必要がなくなります。

但し、配列を拡張できないケースではこの方法は使用できません。

二分探索法

二分探索法は、整列済みのデータの並びを二等分しながら、目的のデータを探す探索アルゴリズムです。

例えば、昇順に整列済みの配列であれば、以下のような流れとなります。

1. 並び全体の中央のデータと目的のデータを比較する。一致すれば終了。
2. 目的のデータが中央のデータより小さければ、前半の部分並びにを対象にして、大きければ後半の部分並びを対象にして、１を繰り返す。
3. 最終的に部分並びの要素が１つになったら、見つからなかったことになる。

なお、二分探索法を行なった場合の探索回数は以下の通りとなり、オーダ記号で表すと O(log₂n) となります。（データは n 個とする）

• 最小探索回数：　１回
• 最大探索回数：　( log₂n)＋１回
• 平均探索回数：　 log₂n 回

例えば、要素の数が65,536個（2¹⁶）であった場合、線形探索法なら、最大で65,536回、平均でも32,768回かかります。
対して、二分探索法の場合、比較を行うたびに、部分並びの数が、2¹⁶、2¹⁵、2¹⁴、・・・2²、2¹、2⁰ と減っていき、最大でも17回で済みますので、二分探索法の方がはるかに高速なアルゴリズムです。

ハッシュ表探索

ハッシュ表探索法は、データの格納位置をデータの値から決めることで、目的のデータを直接得られる方法です。
ハッシュ表という配列の複数の要素に、探索対象の部分並びを所属させておき、目的のデータの値に対してある種の計算を行い、一つの部分並びだけを探索対象として選択する探索アルゴリズムです。

例えば、目的のデータを100で割った余りは、必ず0～99の数になります。この値を100個の要素の配列の索引として、一つの部分並びを選択することが出来ます。
この例の「目的のデータを100で割った余り」といったような、目的のデータを範囲内の値に換算する関数のことを「ハッシュ関数」といいます。

ハッシュ表探索では、最初の1回目の検索で多くの部分並びの中から1つを選択することで、初めの時期の検索回数を減らしています。

ハッシュ関数と衝突

ハッシュ関数を適用した結果、値が重複してしまうことを衝突（シノニム）といいます。

ハッシュ表を使う場合、ハッシュ関数を検討する際に極力シノニムが発生しないようにすることも重要ですが、余りハッシュ表を大きくすると無駄も多いので、シノニム発生時の対処法もあわせて検討しておく必要があります。
例えば、データの件数が１万件だからといって、１万件のハッシュ表を作るのでは、メモリをムダに消費してしまいます。

シノニム対策としては、以下のようなパターンが主流です。

• ハッシュ表の隣接する要素を使う。
• シノニム用の領域を別途用意する。

併合のアルゴリズム

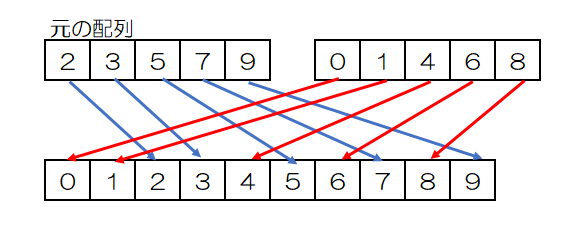
併合のアルゴリズムは、二つの整列済みのデータの並びを一つの整列されたデータの並びにするアルゴリズムです。

1. 二つの配列のそれぞれ先頭の要素を比較して、値の小さい要素を併合先の配列の先頭に移す。
2. 残りの配列について、それぞれの配列の最後の要素を移し終わるまで１の処理を繰り返す。

再帰のアルゴリズム（リカーシブ）

再帰とは、定義自身の一部にその定義が含まれるという性質です。

再帰のアルゴリズムは、反復を含むアルゴリズムと似ていますが、それよりも簡潔になります。

例えば、１からｎまでの自然数の和を表す関数を f( n ) とします。
・ｎ＝１のときは、f(1) は値として「1」を返す。
・ｎ＞１のときは、f( n )は値として「ｎ＋f( n－1 )」を返す。

この関数を使って、１から４までの和を計算する場合、以下のように再帰が進行していきます。

f(4) ＝ ４＋f(3)
　＝４＋３＋f(2)
　＝４＋３＋２＋f(1)
　＝４＋３＋２＋１
　＝１０

再帰のアルゴリズムは、これまでに紹介した整列や探索のアルゴリズム（マージソート、クイックソート、二分探索法）でも活用されているアルゴリズムです。