この記事での学習内容 基本情報 応用情報

グラフのアルゴリズムを理解する。

用語例：深さ優先探索、幅優先探索、最短経路探索

グラフのアルゴリズム

グラフは節（ノード）とそれらを連結する結線（リンク）で結ばれた一つの図です。通信網、木構造、あるいは流れ図がその例です。（木構造の場合は、結線のことを枝とも呼ぶ）

これらのグラフを扱うアルゴリズムをグラフのアルゴリズムといいます。

木の巡回法（再掲）

木構造からデータを探して読み出すことを「木の巡回」といいます。二分木の巡回法には幅優先探索と深さ優先探索があります。

木の幅優先探索

幅優先探索は、階層が浅いデータを優先して検索する方法です。

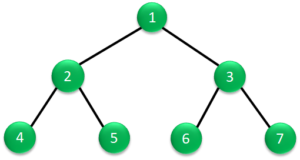
幅優先探索を行うと、最初に子のデータを読み出します。子のデータが検索したデータでない場合は、１階層目の節や葉のデータを左から右へと順番に読み出していきます。１階層目のデータが検索したデータでない場合は、次は２階層目と進んでいく、という方法です。

木の深さ優先探索

深さ優先探索は、左部分木を優先して、階層が下のデータを先に読み出す方法です。

葉以外の節のデータと、葉のデータを読み出す順番の違いにより、先行順探索、中間順探索、後行順探索の３種類があります。

先行順探索

先行順は、節、左部分木、右部分木の順番で読み出す方法です。

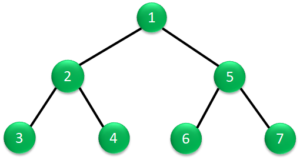
右の図を例にとって説明すると、最初の節である根のデータ１を読み出し、次に左部分木の節のデータ２を読み出します。
その次は２階層目の左部分木のデータ３を読み出します。
３階層目はないので、２階層目の右部分木のデータ４を読み出します。

中間順探索

中間順は、左部分木、節、右部分木の順番で読み出す方法です。

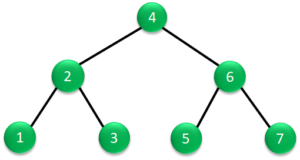
右の図を例にとって説明すると。根から始めて２階層目の左部分木で左部分旗がなくなるので、データ１を読み出します。
次に、上の階層に戻ってデータ２を読み出します。
その次に２階層目の右部分木のデータ３を読み出します。
２階層目の読み出しが終わると、次は根のデータ４を読み出します。

後行順探索

後行順は、左部分木、右部分木、節の順番で読み出す方法です。

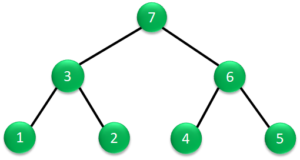
右の図を例にとって説明すると、根から始めて２階層目の左部分木で左部分旗がなくなるので、データ１を読み出します。
次は２階層目の右部分木のデータ２を読み出します。
その次は、上の階層に戻ってデータ３を読み出します。
その次は、１階層目の右部分木ですが、そこからは左部分木が出ているので、左部分木のデータ４を読み出します。

最短経路探索

最短経路とは、グラフのある出発点の節から終着点の節へ到達するのに、結線ごとに要する時間や距離の合計が最短である結線の並びです。この最短経路をたどることを「最短経路探索」といいます。
結線ごとに要する時間や距離を総称して「コスト」といいます。

例：ダイクストラのアルゴリズム

1. 出発点から各説へのコストの表は、出発点の節だけゼロとし、それ以外の節へのコストは初期値として無限大とする。
2. 出発点の節から、結線の一つをたどって、節のデータを調べる。
   1. その節へのコストの記録が、今回の経路のコストより大きいなら、今回の経路のほうが短いので、今回の経路のコストを記録し、直前の節の記号をその節に関するデータとして記録する。（その節へのコストが初期値の無限大だったのなら必ずこちらの処理）
   2. その節へのコストの記録が、今回の経路のコスト以下なら、今回の結線は最短経路に含まれないので、それ以降の処理対象から除外する印を記録する。
3. 以上の処理を、処理していない結線について反復する。
4. すべての処理が終わったら、終着点の節から最短のコストを回答する。また、直前の節を次々と逆行して、出発点から終着点までの節の順序を経路として回答する。