この記事での学習内容 ITパスポート 基本情報 応用情報
整列のアルゴリズムを理解する。
用語例:選択ソート、バブルソート、マージソート、挿入ソート、シェルソート、クイックソート、ヒープソート
整列(ソート)
整列とは、データを大きい順(降順)または小さい順(昇順)になるように並び替えることです。
| 昇順 | 降順 | |
|---|---|---|
| 数値「32514」 | 12345 | 54321 |
| 英字「BDAEC」 | ABCDE | EDCBA |
| かな「いあえおう」 | あいうえお | おえういあ |
数値データは値の大小順に整列され、文字データは文字コードの値の大小順で整列されます。
英字はアルファベット順に、ひらがな、カタカナは50音順に文字コードが割り振られているため、英字同士はアルファベット順、ひらがな同士、カタカナ同士は50音順で並び替えが可能になります。
| 名称 | オーダー(計算量) | 処理速度 | 備考 |
|---|---|---|---|
| バブルソート | O(n2) | 遅い | 処理が単純で実装が容易。 |
| 選択ソート | O(n2) | 遅い | 処理が単純で実装が容易。 |
| 挿入ソート | O(n2) | 遅い | 処理が単純で実装が容易。 O(n2) のアルゴリズムの中では高速。 |
| シェルソート | O(n1.2)~O(n2)程度 | やや遅い | 挿入ソートの改良版だが、場合によっては挿入ソートと速度が変わらない。 |
| マージソート | O(n log2n) | 高速 | 「再帰」の概念の理解が必要。 |
| クイックソート | O(n log2n) | 高速 | 「再帰」の概念の理解が必要。 |
| ヒープソート | O(n log2n) | やや高速 | 「ヒープ木」の概念の理解が必要。 |
バブルソート
代表的な整列のアルゴリズムに、バブルソートがあります。バブルソートは一つとなりと比べては入れ替える、という処理を繰り返していく方法です。
隣同士のうち、大きい方が前に並ぶように入れ替えていくと、結果的に全体が降順で並びます。逆に小さいほうが前に並ぶようにすると昇順となります。
例:「1・5・7・3・9」の5枚のカードをバブルソートで降順に並び替える。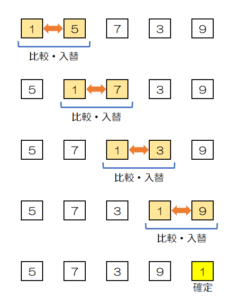
- 要素[1]と[2]を比較して、大きい方が前になるように入れ替える。
- 続いて[2]と[3]、[3]と[4]、[4]と[5]の順に比較と入れ替えを行う。
この時点で、要素[5]が最小値になるので、要素[5]の位置が確定する。 - 要素[1]~[4]について、同様に比較と入れ替えを繰り返し、各要素の位置を確定する。
バブルソートの計算量
n個の要素をバブルソートで整列する時の比較の回数は、 ( n ( n - 1 ) ) ÷ 2 であり、n の2乗に比例します。。
オーダ記号で表すと、O(n2) となります。
選択ソート
選択ソートは、最小値の要素を選択して、先頭の要素と置き換える整列アルゴリズムで、基本選択法ともいいます。
処理効率は、バブルソートと変わらず、計算量はO(n2) となります。
例:「1・5・7・3・9」の5枚のカードを選択ソートで昇順に並び替える。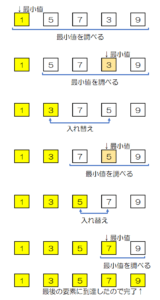
- 要素[1]~[5]の値を調べて、最小値を求める。
- 1.で求めた最小値を先頭の要素と交換する。
- 残りの要素について、1と2を繰り返す。
挿入ソート
挿入ソートは、前の方の整列済みの並びの途中へ、直後の要素を挿入する整列アルゴリズムで、基本挿入法ともいいます。
計算量はO(n2) となります。
例:「1・5・7・3・9」の5枚のカードを挿入ソートで昇順に並び替える。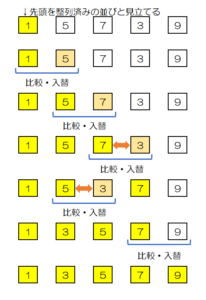
- 先頭の要素を1要素だけの整列済みの並びと見立てる。
- 整列済みの並びの要素と、その直後の要素を比較して、バブルソートと同じ要領で並び替えを行う。
- 最後の要素を処理するまで、2を繰り返す。
マージソート
マージソートは、並びを2等分しながら、分割された部分同士を併合(マージ)することによって、全体を整列させるアルゴリズムです。
例:「2・7・5・3・8・1・4・6」の8枚のカードをマージソートで昇順に並び替える。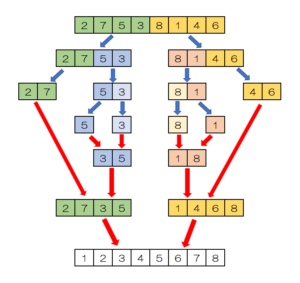
- 並びを2等分することを、整列済みの部分並びが見つかるまで反復する。(要素が1つになれば整列済みとみなすので、反復は必ず終了する。)
- 整列済みの部分並び同士を、整列状態を保つように併合して、1つの部分並びにする。
- 全体が1つの部分並びになるまで、2を反復する。
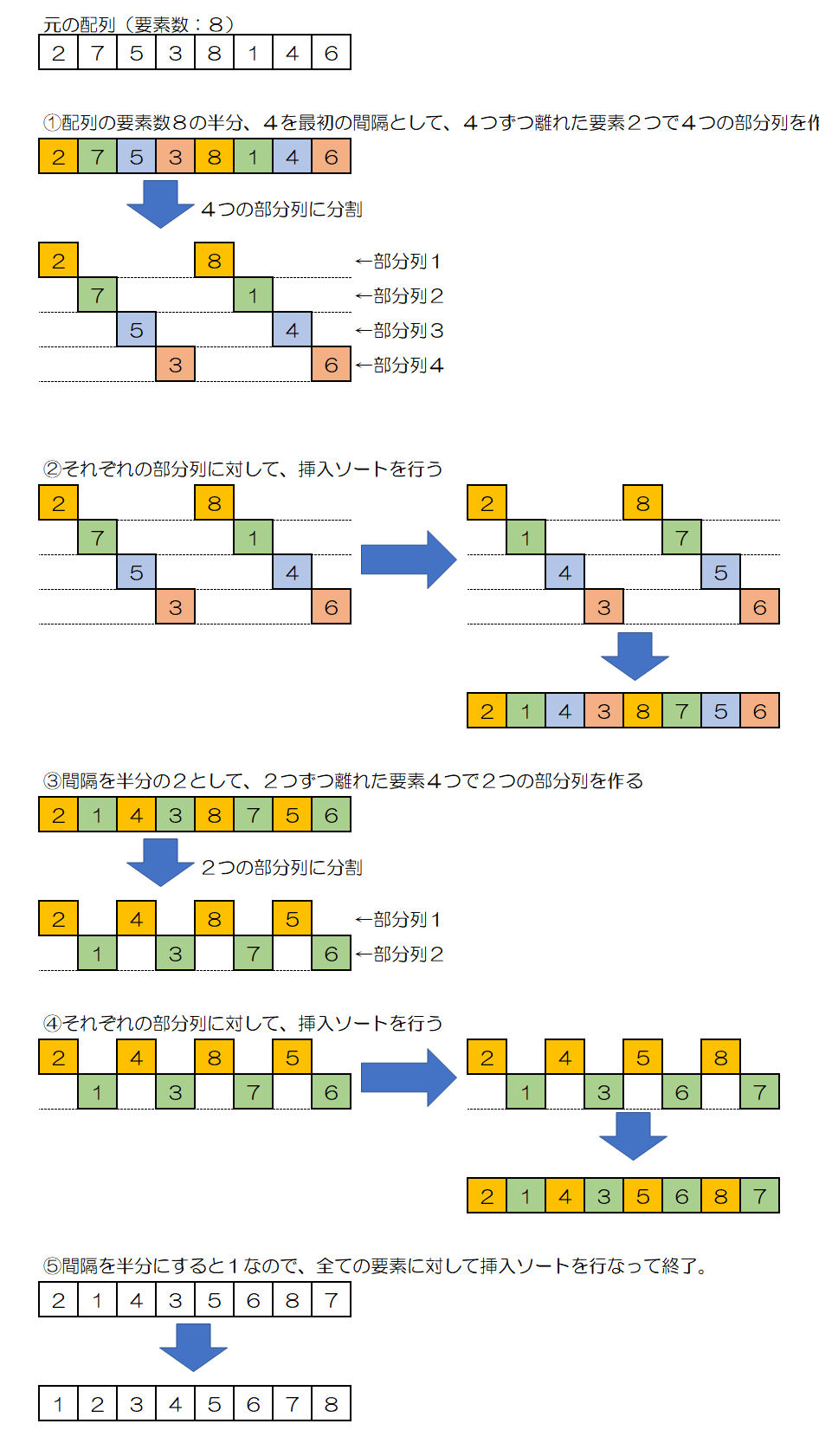
シェルソート
シェルソートは、シェル氏によって考案された挿入ソートの改良版の整列アルゴリズムです。
- 適当な間隔を決めて、等間隔の飛び飛びの要素で作った部分的な並びに対して挿入ソートを適用する。
- 間隔を狭めながら、間隔が1になるまで1を繰り返す。
例:「2・7・5・3・8・1・4・6」の8枚のカードをシェルソートで昇順に並び替える。
挿入ソートは、元々の並びが整列状態に近いほど高速になる性質があるため、間隔を空けて部分的な並びを作って徐々に整列させることで速度の向上を図っています。
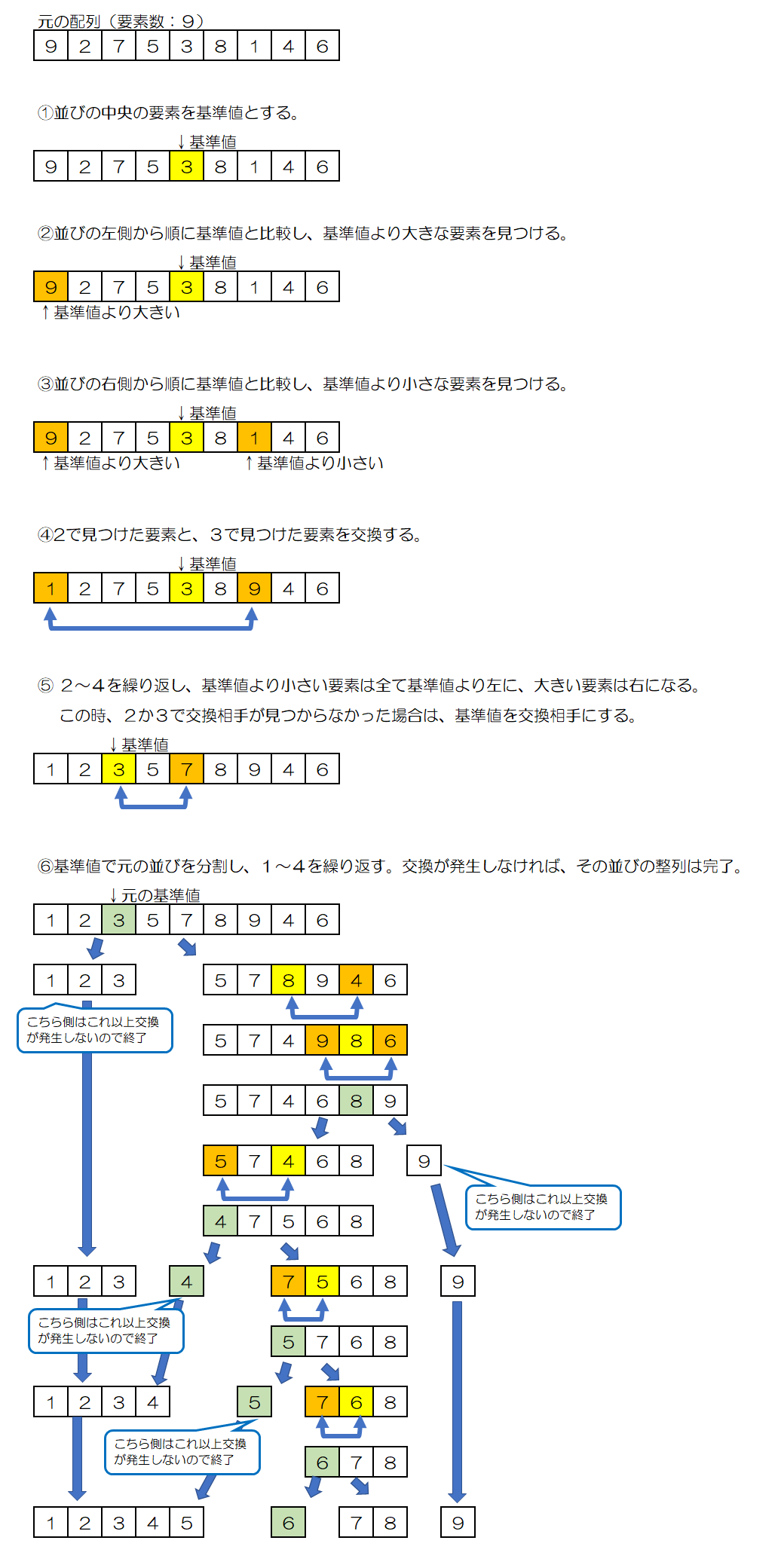
クイックソート
クイックソートはその名の通り、特に高速な整列アルゴリズムです。
- 適当な基準値を定めて、その値より小さい要素を前の方に移し、その値以上の要素を後の方へ移す。
- 分割したそれぞれのグループへ、1の処理を反復して、全てのグループに属する要素数が1になるまで繰り返す。
例:「9・2・7・5・3・8・1・4・6」の9枚のカードをクイックソートで昇順に並び替える。
反復する毎に、分割されたグループの数は2倍、4倍、8倍というペースで増えていくので、各グループに含まれる要素の数は急激に減っていきます。
基準値と要素の値を比較する回数が急速に減っていくことが、クイックソートが特に高速である理由です。
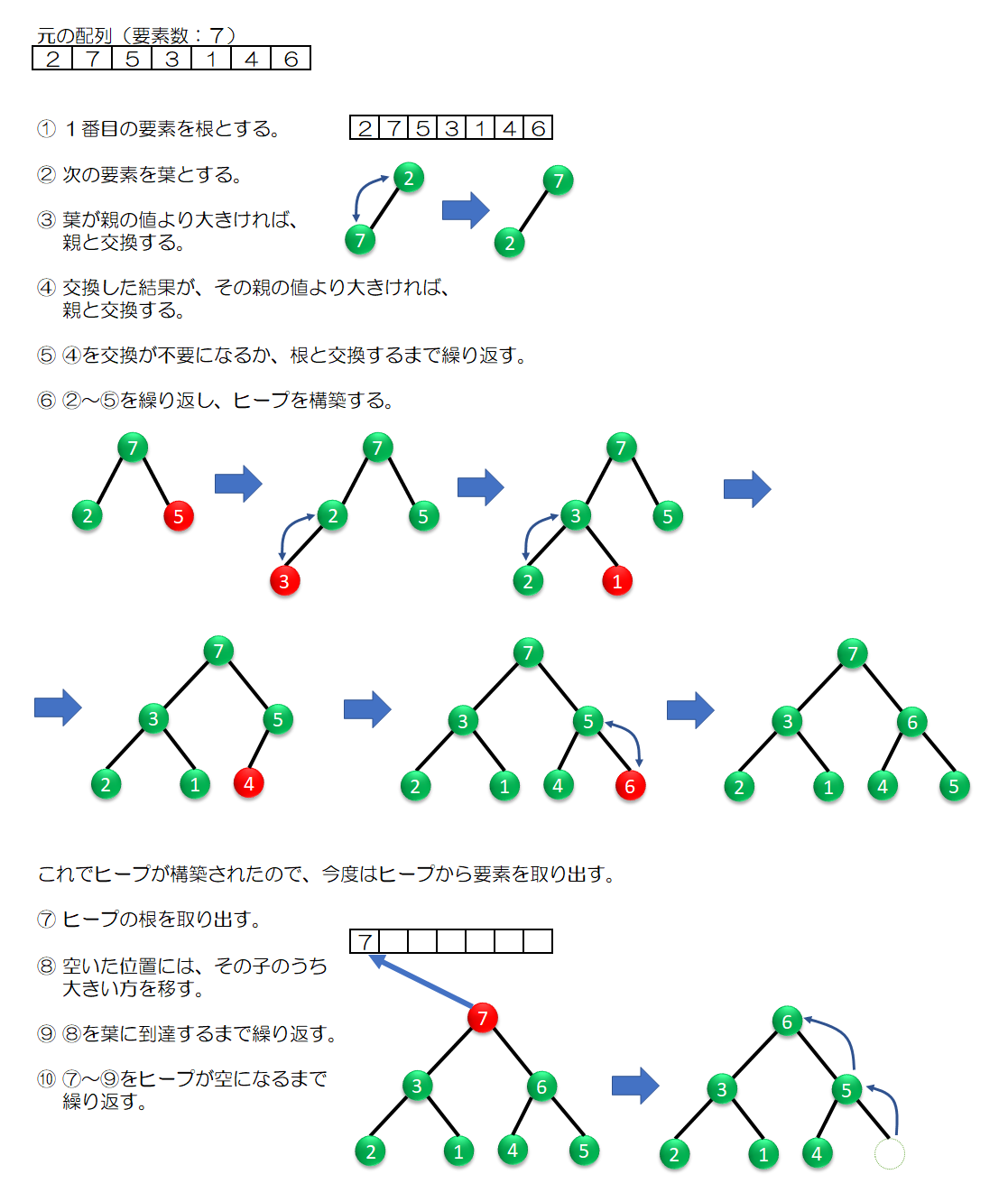
ヒープソート
ヒープソートは、ヒープを経由する整列アルゴリズムです。
ヒープは「小さい山」という意味の言葉であり、親の値が必ず子の値以上であることを保つ二分木です。
- 要素の並びを元にして、ヒープを構築します。子の処理には、木構造アルゴリズムの一種である、ヒープ構築アルゴリズムを用います。
- 根に当たる要素を取り出して、並びの端へ移します。
- ヒープに残った要素に対して、ヒープ再構築アルゴリズムを適用します。
- 2と3をヒープの要素がなくなるまで繰り返します。
例:「2・7・5・3・1・4・6」の7枚のカードをヒープソートで降順に並び替える。
二分木は木の階層ごとに、部分木の数が2倍、4倍、8倍と増えていきます。値の大小比較の回数は2つの部分木の根を比較するだけなので、ヒープソートは特に高速とされています。