この記事での学習内容 ITパスポート 基本情報 応用情報
待ち行列理論の構成要素、考え方、M/M/1モデルにおける計算、乱数を利用したシミュレーションを理解する。
用語例: サービス時間、到着間隔、平均到着率、平均サービス率
待ち行列モデル
我々の生活の中では、銀行のATMや行政の窓口、商店のレジなど色々なところで行列が作られています。この待たされる行列のことを待ち行列と呼びます。この顧客がサービスを受けるために行列に並ぶ時の、待っている人の人数や待ち時間などを解析するための理論を待ち行列理論といいます。
この理論の中で、特に顧客とサービス窓口、待合室からなるシステムを「待ち行列モデル」として扱っています。
待ち行列モデルには種類がありますが、この種類を表す方法として、1953年にケンドール氏によって提案されたケンドール記号があります。ケンドール記号はA/B/Cという形式で表され、
A:到着時間の分布の種類
B:窓口を利用する時間(サービス時間)の分布
C:窓口の数
となります。
到着時間の分布の種類は、殆どの事象はランダムに到着するので、記号は M を使います。(マルコフ過程のM)
サービス時間の分布は、サービス時間が短い場合が多く、サービス時間が長い場合はそれほど多くないといった事象が一般的で、指数分布のグラフを取ります。
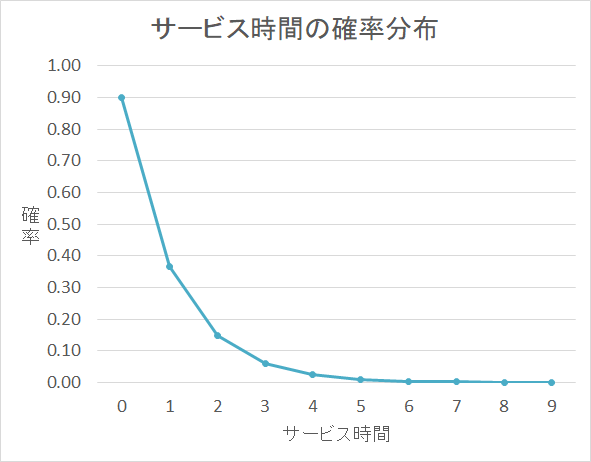
サービス時間の分布が指数分布に従っている場合は、記号はMと表します。
窓口の数は、ネットワークやCPUを待ち行列理論で扱う場合は、窓口が1つのモデルが良く使われます。
これに従って、銀行ATMや売店のレジなどの待ち行列モデルで、窓口が一つのモデルをケンドール記号で表すと、M/M/1となり、「M/M/1モデル」と呼ばれます。
M/M/1モデルでの計算
M/M/1モデルでの、平均待ち時間などを求めるための必要な計算式は下記のとおりです。
- 平均到着率: λ (ラムダ)
単位時間あたりに到着する顧客の数 - 平均到着時間: ta (time arrival)
ta = 1 / λ - 平均サービス率: μ (ミュー)
単位時間に窓口が処理できる件数 - 平均サービス時間: ts (time service )
窓口における一人にかかるサービス時間
ts = 1 / μ - 平均利用率: ρ (ロー)
窓口をどれだけ利用しているかの割合で0~1の値。
ρ = λ × ts または ρ = λ / μ
ρが1以上になってしまう場合、到着時間よりも処理時間が長いことになり、待ち行列が延々と伸び、いつまでたってもサービスが受けられない状況を表します。 - 平均待ち時間: tw (time wait)
待ち行列に並んでからサービスが開始されるまでの時間
tw = ρ / (1 – ρ) ×ts - 平均応答時間:T
行列に並んでから、窓口でのサービスが完了するまでの時間
T = tw + ts
例:とある行政の窓口で、1時間あたり10人の利用者があり、その窓口では1時間で15人の利用者に対応できる場合の平均待ち時間、平均応答時間を求める。
- 文章から、単位時間は1時間とし、λ = 10、μ=15となる。
- 平均サービス時間を求める。ts=1/μ なので、
ts=1/15 (=4分) - 平均利用率を求める。ρ = λ / μ なので、
ρ = 10 / 15 = 2/3 - 平均待ち時間を求める。tw = ρ / (1 – ρ) ×ts なので、
tw = (2/3) / (1 – 2/3) ×1/15 =(2/3) / (1/3) × 1/15 = 2 × 1/15 =2/15 となり、2/15時間=8分。 - 平均応答時間を求める。T = tw + ts なので、
1 / 15 + 2 / 15 =3 / 15 となり、3/15時間=12分。