この記事での学習内容 基本情報 応用情報
二分法、補間法、オイラー法など、近似解を数値的に求める考え方や計算過程で生じる誤差を理解する。
用語例: 数値積分、シンプソン法、ニュートン法、絶対誤差、相対誤差、丸め誤差、打切り誤差
数値解析とは、物理学、数学、工学などの科学分野の問題を、方程式を解くのではなく、数値計算を行なって解の近似値を求める手法のことです。
数値解析は、コンピュータを使った様々なシミュレーションなどに用いられています。数値計算、実用解析などとも呼ばれます。
二分法
二分法は、方程式の一つの実数の解を求める時に、解を含む区間を二分して中間点を求め、二分したどちら側に解が入るかを判定し、再度範囲を二分して判定する作業を、何度も何度も繰り返して、解の値を求めていく方法です。
方程式 f(x) = 0 の解を求める時に使用される代表的な数値解析方法の1つで、解のおおよその値を知っていることが前提です。
ニュートン法
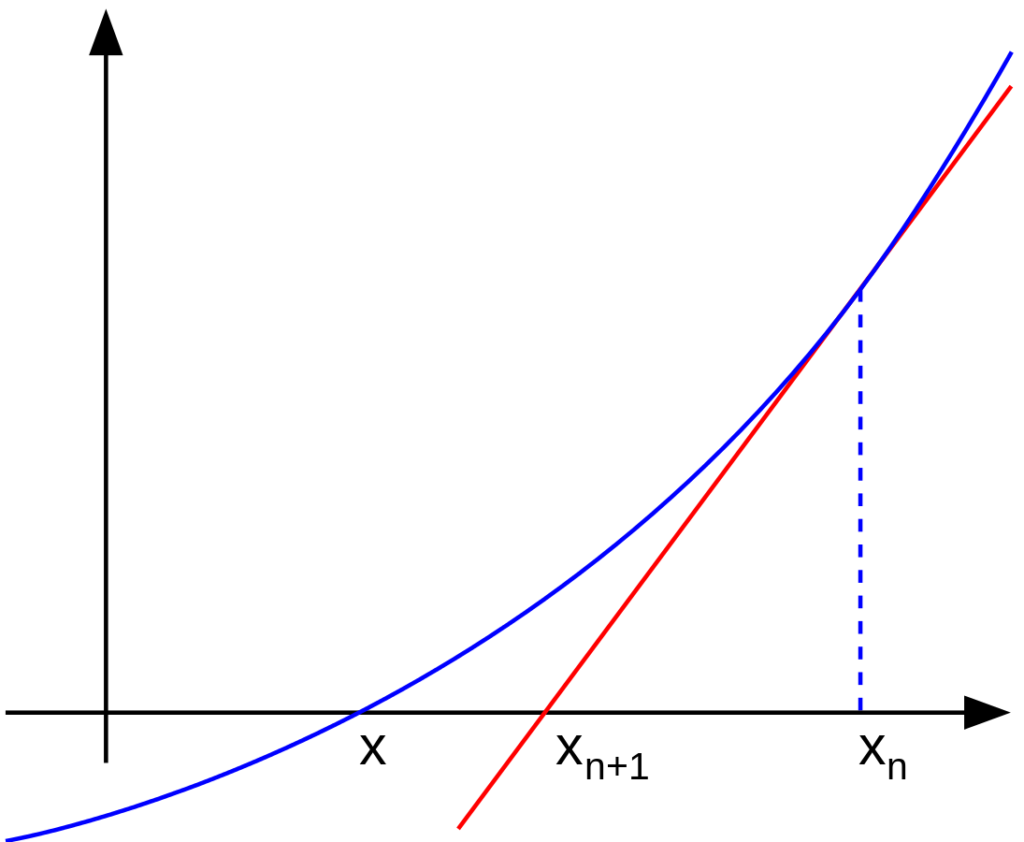
ニュートン法は、グラフの形がなだらかに変化している場合に有効な方法です。
下図の様にグラフの形がなだらかな場合、ある値の接線とx軸の交点を取ると、もとの値より、グラフのx軸の交点に近づきます。
これを繰り返して、 f(x) = 0 の解を求める方法です。
補間法
補間法とは、グラフ上の複数の点を通る多項式の曲線で、xの値からyの値を計算することです。
補間法には何種類かの計算方法がありますが、代表的な方法として、ラグランジュ補間法やスプライン曲線などがあります。
ラグランジュ補間法
すべての点を通過する数式を求める方法。データの点数が増えると、曲線の振れ幅が大きくなってしまうという欠点がある。
スプライン曲線
ラグランジュ補間法の欠点を補うために、データを一定の区分で区切った上で、近似する曲線を予測していく方法。
誤差
数値解析で求めた解の値は、あくまでも近似値です。本島の海の値である「真値」との差があり、この差を「誤差」と呼びます。
数値解析の誤差には、絶対誤差、相対誤差、打切り誤差があります。
絶対誤差、相対誤差
真の値(真値)と測定値や近似値との差を誤差といい、この時
絶対誤差=測定値(近似値)- 真値
相対誤差=絶対誤差 ÷ 真値
となっています。
例えば、真値が1000mmで、測定値が998mmだった場合、
絶対誤差は、998 - 1000 = -2mm、
相対誤差は、 -2mm ÷ 1000mm = -0.02 = -2%
となります。
丸め誤差、打切り誤差
計算の結果を指定した桁数で収めるために、最下位の桁を切り捨て、切り上げ、四捨五入などをすることで生じる誤差を「丸め誤差」といいます。
また、計算を途中で打ち切ってしまう場合も真の値とは誤差が出ることになります。この途中で打ち切った時に出る誤差を「打切り誤差」といいます。打切り誤差の例としては、円周率の計算などがあります。