この記事での学習内容 ITパスポート 基本情報 応用情報
集合,命題,ベン図の手法と考え方を理解する。
用語例: 和集合,積集合,補集合,部分集合,真,偽,命題論理
集合
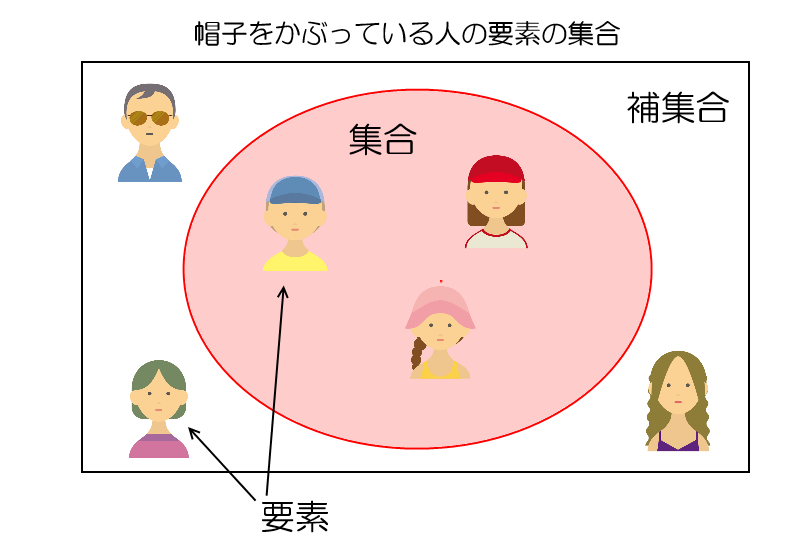
集合とは、同じ属性を持つ要素の集まりのことです。
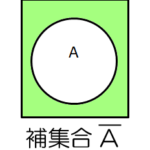
集合はよく「ベン図」で表されます。要素全体の集まりを四角で表し、そのうち集合に含まれる要素を色付きの円で示します。この時、集合に含まれない円の外側のことを補集合といいます。
集合演算
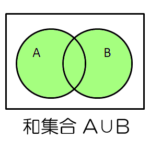
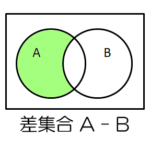
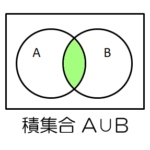
集合同士を演算することを集合演算といい、「和集合」「差集合」「積集合」が代表的です。
| 演算 | 意 味 | 式 |
|---|---|---|
| 和集合 | 集合と集合を足す | |
| 差集合 | ある集合から、別の集合と共通する部分を引く | |
| 積集合 | 複数の集合から、互いに共通する部分を取り出す | |
| 補集合 | 全体から、その集合を取り除く |
集合の包含関係
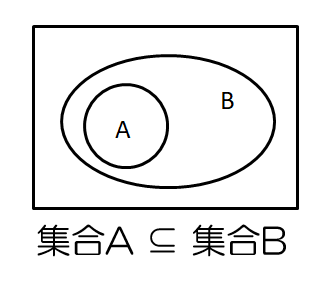
2つの集合の関係は、場合によっては下図のように、集合Aが集合Bに含まれる場合もある。この様な包含関係を表す演算子として「⊆」や「⊇」が用いられる。
命題
命題とは、要素を「正しい(真)」か「正しくない(偽)」かで振り分けるための条件付けを指します。ある命題について、真か偽かによって要素を振り分けると集合を作ることが出来ます。
また、「真」と「偽」を真理値といい、「真」を1、「偽」を0として表すこともあります。対象となる要素の真理値を表の形にまとめたものを、真理値表といいます。