この記事での学習内容 ITパスポート 基本情報 応用情報
負の数の表現(補数表現)を理解する。
用語例: BCD (Binary Coded Decimal:2 進化 10 進),パック 10 進数
2進数における表現の問題点
整数の場合は桁数が多くなる程度ですが、小数の場合はそもそも表現できる数が少ないため、どうしても「誤差」が生じてしまいます。
例えば、10進数の 0.75 は、2進数で 0.11 と表すことが出来ますが、10進数の0.7を2進数で表そうとすると、 0.1011011… と延々と続く「無限小数」となってしまい、2進数で表すことが出来ません。
こういった数を表そうとすると、一定の桁で打ち切って表現せざるを得ません。しかし、打ち切ると10進数に戻した時にもとの値に戻すことが出来ず、「誤差」が生じてしまいます。
例えば、先述の 0.7 を2進数で表現し、小数第6位までで打ち切ったとすると、0.101101 となります。これを再度10進数に戻すと、0.64275 となり、元の 0.7 には戻せません。
打ち切る際に出来るだけ桁数を多く取れば誤差を減らすことは出来ますが、誤差を無くすことは出来ません。
10進数に近い形で数値を表現する方法
コンピュータ内部で扱われるデータは2進数が使われますが、コンピュータに入力される数値は10進数の場合が多いため、単純に2進数に変換しただけだと、誤差が発生しやすくなります。
その為、10進数の値を2進数に変換せずに表現する方法が考えられてきました。ゾーン10進数とパック10進数です。
ゾーン10進数は1桁を8ビットで表現し、パック10進数は1桁を4ビットで表現します。
いずれも、10進数書く桁の数字を4ビットの2進数で表現したBCDコードというものを使います。
BCDコード
BCD : Binary Coded Decimal の略。
BCDコードとは、10進数の各桁の数字を4ビットの2進数で表したもので、10進数を2進数に変換し、4ビット中の残りの上位ビットに0を入れたものです。
| 10進数 | BCDコード |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
なお、BCDコードで表現した2進化10進数といいます。
ゾーン10進数(アンパック10進数)
ゾーン10進数は8ビット(=1バイト)で10進数1桁を表現する方法です。8ビットを上位4ビットのゾーン部と、下位4ビットの数値部に分け、数値部は先述のBCDコードを使って表します。
なお、ゾーン部の値は、汎用コンピュータなどで使われるEBCDIC方式では「1111」、JIS方式では「0011」が用いられます。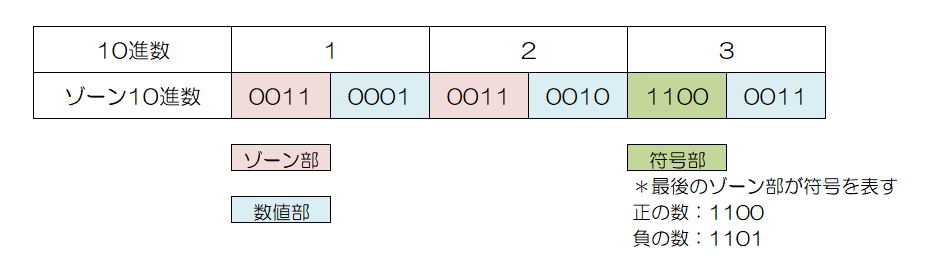
ゾーン10進数で10進数を表現する場合、数値の桁数分のバイト数が必要となり、格納効率はよくありません。しかし、数字を表す文字コードとの相性が良く、数値と文字の変換が行いやすくなっています。
パック10進数
パック10進数は8ビット(=1バイト)で10進数2桁を表現する方法です。8ビットを4ビットずつに分けて数値部とします。
数値部はゾーン10進数と同様にBCDコードを使って表します。
さらに、最下位の4ビットを符号部とし、符号を入れます。
パック10進数はゾーン部を省略してまとめてパックしたイメージとなります。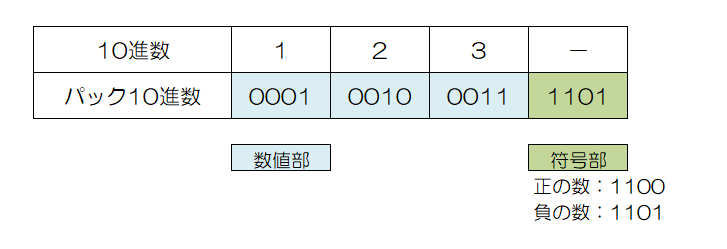
パック10進数で10進数を表現する場合には、桁数の約半分のバイト数が必要で、ゾーン10進数と比べると格納効率にまさり、計算などに適しています。
2進数での符号付きの数の表現方法
正負の数を2進数で扱うためには、プラスかマイナスかを示す符号用に1ビット分を使います。この際、先頭のビットが0ならば正の数、1ならば負の数とするのが一般的です。
具体的な方法としては、以下の3つの方法が用いられています。
| nビット使った場合の表現範囲 | 例)5と-5を8ビットで表した場合 | |
|---|---|---|
| 絶対値に符号をつける | -2n-1-1 ~ 2n-1-1 8ビットの場合:-127~127 | 5(10) → 00000101(2) -5(10) → 10000101(2) |
| 1の補数を用いる *負数の場合、絶対値のビットを全て反転させる | -2n-1-1 ~ 2n-1-1 8ビットの場合:-127~127 | 5(10) → 00000101(2) -5(10) → 111111010(2) |
| 2の補数を用いる | -2n-1 ~ 2n-1-1 8ビットの場合:-128~127 | 5(10) → 00000101(2) -5(10) → 111111011(2) |
この内、絶対値に符号を付ける方法と1の補数を用いる方法の場合、「+0」と「ー0」という同じ値が2つの方法で表現されてしまい、僅かにですが同じビット数で表現できる数値の範囲が少なくなってしまいます。
限られたビット数でできるだけ広い範囲の値を表現したいコンピュータにとっては余り良い方法ではないため、2の補数を用いる方法が一般的となっています。
2の補数による負数の表現
補数とは、「補う数」と言う名のとおり、それを足すとちょうど桁上りの基準値になる数のことです。
10進数の場合、基数が10nなので、7にとっての10の補数は4、8にとっての10の補数は2となります。
2進数の基数は2nなので、例えば 110(2) の2の補数は、足すと桁上りして 1000(2)になる数のことなので、計算すると 10(2)と求められます。
110(2) の2の補数 = 1000(2) - 110(2) = 10(2)
なお、2の補数は「元の数のビットを全て反転し、1を足す」という方法で簡単に求められます。この方法の場合、結果的に負の数の先頭ビットが常に0になるため、先頭ビットが符号ビットの役割も果たします。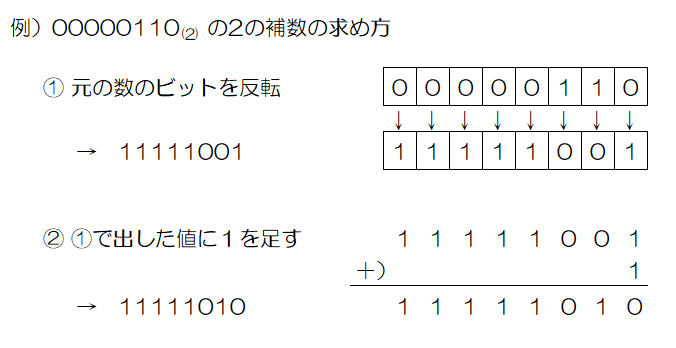
補数を使った減算
負数を扱う時に「2の補数」を用いると、限られたビット数で表現できる値の範囲が広くなるメリットの他に、「引き算を足し算の仕組みのままで計算できる」というメリットがあります。
一般的な10進数の計算でも、式を変形して以下のように引き算の式を「負数による加算」とすることが出来ますが、考え方は同じです。
例) 6 – 2 = 6 + ( -2) = 4
同様に、2進数の引き算を「負数による加算」で行なってみます。解が正数になる場合、負数になる場合両方を見てみましょう。
*今回は8ビットを使って正負の整数を表すものとします。
負数を2の補数で扱うことで、コンピュータにとっては加算命令だけで足し算も引き算もできるようになるため、演算機能が簡略化出来ます。
人間が2の補数で計算する際には、「最上位で桁上りしたビットは無視する」という手順が必要になりますが、コンピュータの場合、「整数を8ビットで表す」としている場合、桁上りして発生した最上位の9ビット目は無視されてしまうため、わざわざ「最上位で桁上りした場合」ということを考える必要も無いのです。