この記事での学習内容 ITパスポート 基本情報 応用情報
順列、組合せ、場合の数、確率とその基本定理、確率分布(離散型、連続型)と期待値、マルコフ過程を理解する。
用語例:階乗、加法定理、乗法定理、正規分布、ポアソン分布、指数分布、カイ二乗分布、確率密度
場合の数
ある出来事が起きる可能性の数を「場合の数」と呼びます。場合の数で数えられる「ある出来事」は「事象」と呼びます。
例えば、サイコロを一個転がす場合を考えると、場合の数は6です。サイコロが2個になれば、場合の数は 6 × 6 で36です。

順列
箱の中に赤、青、黄の3種類の玉が1個ずつあるとします、この中から2個を選んで、順番に並べる場合、次の6通りの順番が考えられます。
| 1個め | 赤 | 赤 | 青 | 青 | 黄 | 黄 |
| 2個め | 青 | 黄 | 赤 | 黄 | 赤 | 青 |
この例のように、複数あるものから幾つかを選んで、順番を付けて並べる時の並べ方を「順列(Permutation、パーテーション)」といいます。n 個の中から r 個取って並べる順列を、nPr と表します。
順列の個数は計算で求めることが出来ます。
上の例では、1個めの玉の色は赤、青、黄の3通りあり、2個めは残りから取るので2通りあります。
1個めの3通りに続いて、2個めの2通りのとり方が並ぶと考えられるので、全部で 3×2=6 通りの順列となります。
同じ要領で、10個のうちから3個選ぶ順列は 10×9×8 = 720通りあります。
n 個の中から r 個取って並べる順列は、以下の公式で求められます。
nPr = n × (n-1) × ・・・× (n-r+2) × (n-r+1)
階乗とは、以下のように 値を n から 1まで、全て掛け算する計算のことです。
n! = n × (n-1) × ・・・× 2 × 1
公式を使って、10個の中から3つを選んで順に並べる順列を求めると、以下のようになります。
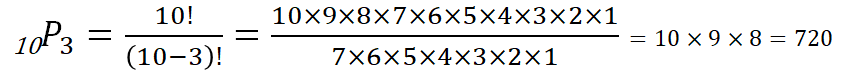
組合せ
複数あるものから幾つかを選んで、順番を付けずに一組にする時のまとめ方を「組合せ(Combination、コンビネーション)」といい、 n 個の中から r 個を取ってまとめる組合せを nCr と表します。
例えば、赤、青、黄の3種類の玉(1個ずつ)の中から2個を選んで組にする場合、「赤、青」「赤、黄」「青、黄」の3通りの組み合わせができます。
順列の場合と違い、「赤、青」と「青、赤」は同じ組み合わせとみなします。
組合せの数を求めるには、以下の公式のように、全体の順列を取った数の順列でわれば求められます。
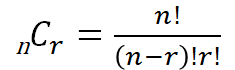
公式を使って、10個の中から3つを選んだ組合せの数を求めると、以下のようになります。
確率
ある出来事が起きると期待できる割合を確立(Probability)といい、事象Aの起こる確率を P(A) と表します。
例えば、1個のサイコロを投げて、「1」の目が出る確率は次のように求めます。
- 全ての目の数は1~6の6通り
- そのうち、「1」の目は1つだけ
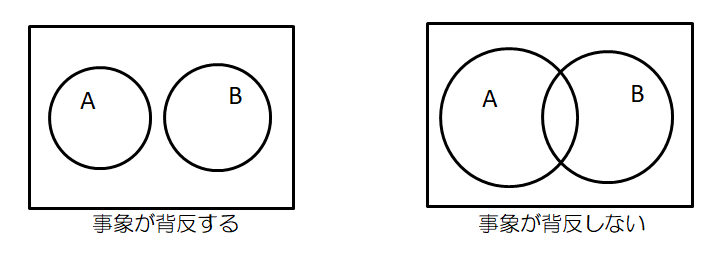
事象の排反
同時に起こりえない事象同士のことを、『事象排反する』という。
ベン図を書いた時に重なる部分がなかったり、論理積をとった時に解が空集合になる場合。
例えば、サイコロを振って『出目が2である』という事象と、『出目が3である』という事象は同時には発生し得ないので、事象が背反している。
が、『出目が2の倍数である』という事象と『出目が3の倍数である』という事象は、出目が6になったときに、ともに条件を満たすので、これらの事象は背反しない事になる。
事象の独立
二つの事象の発生確率を考えた場合、
- 互いに影響しない→事象が独立している。
例)サイコロを続けて振った場合の出目、ルーレットで特定の数字が出る確率など - 他方に影響を与える→事象が独立していない
例)あたり数に限りのあるクジ引きで、1人目が当たる確率と、2人目が当たる確率。
*独立と排反の違い
独立している→互いに影響しない
背反している→同時に発生しない
確率の和事象(加法定理)
事象A又は事象Bが起こることを「和事象(A ∪ B)」といいます。
和事象の起こる確率は事象Aの起きる確率と事象Bの起きる確率を足したものから、事象AとBの積事象の確率を引いたものです。
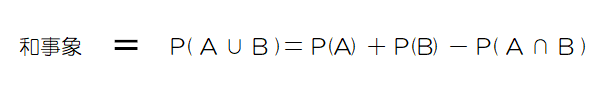
例えば、サイコロを2回投げ、1回目に偶数の目が出る場合と、2回めに「2」が出る場合のいずれか、又は両方が起こる確率は以下のように求めます。

確率の積事象(乗法定理)
互いに独立した事象であるAとBがともに起こることを、事象AとBの積事象( A ∩ B)と言います。
積事象の起こる確率は事象Aの起きる確率と事象Bの起きる確率を掛けたものです。

例えば、サイコロを2回投げる時、1回目に偶数の目が出て、なおかつ2回目に「2」が出る確率は次のように求めます。

(参考)事象が独立していない場合に、事象Aが起きたという条件下で、事象Bが起きる確率は、以下のように求める。

マルコフ過程
時間とともに確率が変化する過程を「確率過程」と呼びます。例えば、降水確率は時間とともに確率が変化するので、確率過程とみなせます。
確率過程の中で、確率の値が過去の状態に一切関係がないものを「マルコフ過程」といいます。
例えば、サイコロを振り続ける場合にある目が出る確率過程を考えます。
現在のサイコロの目が出る確率は、過去のサイコロの目の影響を一切受けないので、マルコフ過程となります。
これに対して、降水確率は現在の降水状況に影響を受ける確率過程なのでマルコフ過程にはなりません。
- 確率過程を取る例:株価、為替、電子回路に対するノイズの発生確率、降水確率など
- マルコフ過程を取る例:サイコロ、ルーレット、宝くじの当選番号
確率分布
ある事象が起きる確率が変数によって決まる場合、変数と確率の関係を「確率分布」と呼びます。
例えば2個のサイコロを降る場合を考えます。
目の数の合計が2になるのは、1と1の場合だけなので、36分の1の確率です。
目の数の合計が3になるのは、1と2,2と1の2つの場合なので、18分の1です。
したがって、この場合は目の数の合計を変数とする確率分布が考えられます。
| 出た目の和 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 確率 | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
なお、確率分布にはサイコロの目のように確率変数が離散的な値を取る場合と、連続する値を取る場合があります。
- 離散型の確率分布:二項分布、ポアソン分布など(サイコロの目など、確率変数がとびとび)
- 連続型の確率分布:正規分布、指数分布など(ある人の身長・体重など、確率変数の小数点以下をいくらでも細かく取れる場合)
ポアソン分布
単位時間中に平均でλ 回発生する事象が、ちょうど k 回(k は0を含む自然数)発生する確率をグラフに取ると、λ = k となる時にピークが来るようなグラフになる。
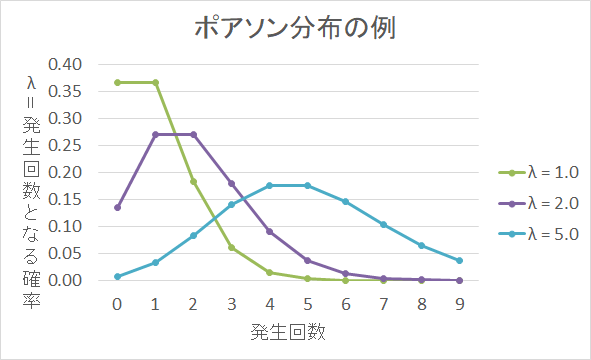
例:1時間に5人の利用者があるATMで、実際に1時間にATMを利用した人数の分布。
指数分布
単位時間中に平均でλ 回発生する事象が、「次に発生するまでの時間」の分布。

例:1時間に5人の利用者があるATMで、次にATMを利用する人が来るまでの時間の分布。
カイ二乗分布
独立に標準正規分布に従う k 個の確率変数 X1, …, Xk をとる。 このとき、統計量 の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。この分布は自由度 k に応じて下図のような形をとる。
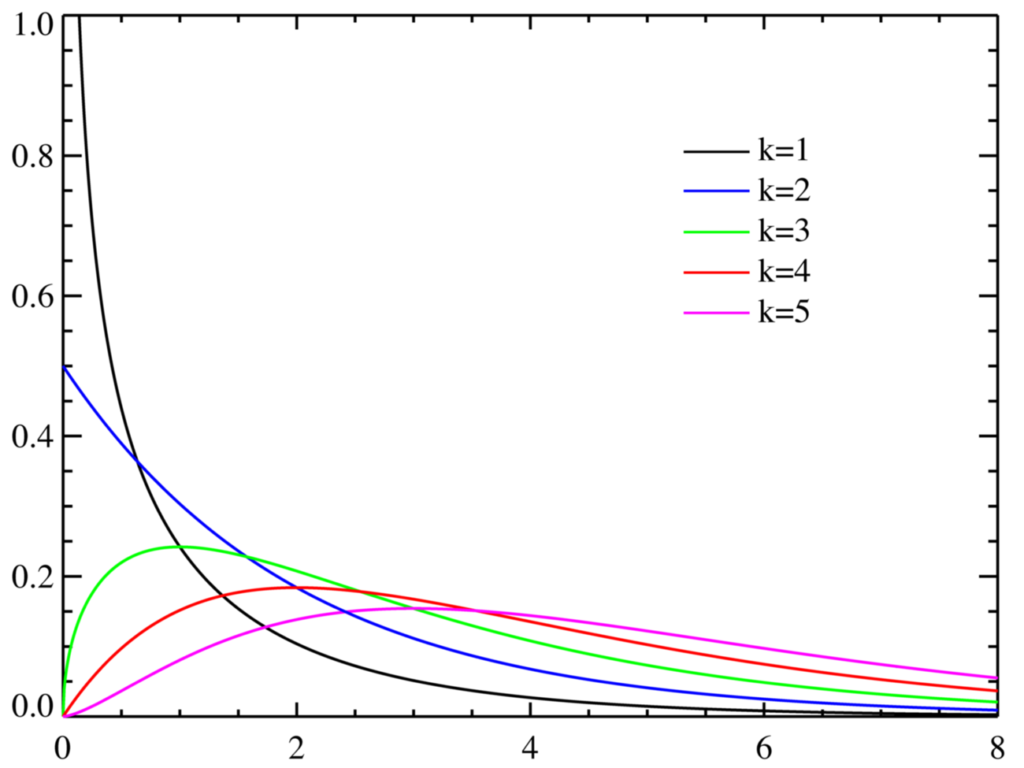
実際に様々な観測データを取得した場合、その分布には誤差が含まれるため、理論的に求められる分布と完全には一致しない。例えば、サイコロの各目の出る確率は1/6であるが、だからといってサイコロを6回振ったら各目が1回ずつ出るわけではない。フル回数を多くすればおおよそ1/6ずつに近い分布になると思われるが、均等に1/6ずつにはならない。
こういった時に「実際の観測データが理論値の分布にほぼ等しいとみなせるかどうか」を分析する際に、カイ二乗分布が用いられる。(この分析方法のことを「カイ二乗検定」とよぶ)
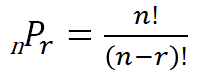
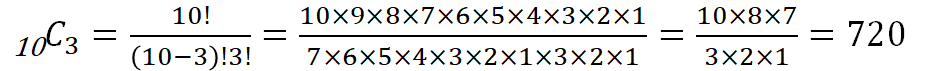

 の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。この分布は自由度 k に応じて下図のような形をとる。
の従う分布のことを自由度 k のカイ二乗分布と呼ぶ。この分布は自由度 k に応じて下図のような形をとる。