この記事での学習内容 基本情報 応用情報
加減乗除,表現可能な数値の範囲,シフト演算,演算精度(誤差とその対策)など,コ ンピュータでの算術演算を理解する。
用語例: 論理シフト,算術シフト,桁落ち,情報落ち,丸め,打切り,オーバフロー(あ ふれ),アンダフロー,単精度,倍精度
シフト演算
引き算は2の補数を使うと足し算で同じ計算が出来ましたが、掛け算や割り算の場合はどうでしょうか。
例えば、10進数の123を10倍すると1230に、100倍すると12300になりますが、この計算は123の桁を10倍のときは1つ、100倍のときは2つ左ずらすことで簡単に求めることが出来ます。
逆に、10分の1にする場合は右に1つ、100分の1にする場合は右に2つずらすことで求めることが出来ます。

つまり、数値の桁を1つずつずらすことは、その数値の『基数倍』や『基数分の1』を計算するのと同じ効果があります。
このように桁を左や右にずらすことを『シフト』といいます。左にずらすことを「左シフト」、右にずらすことを「右シフト」といいます。
これらのシフト演算は掛け算や割り算の代わりに利用することもありますが、通常は2進数でビットバターンの特定の操作をしたり、ビットの状態を判定する際に利用します。
2進数のシフト演算
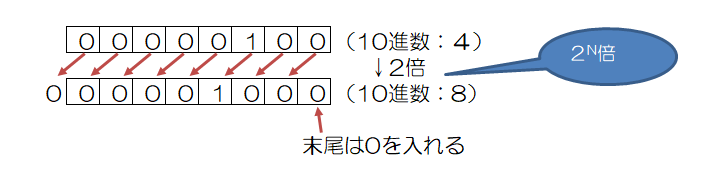
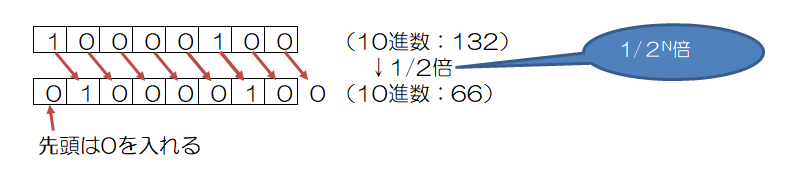
2進数の場合は、1桁左シフトすると数値は2倍、1桁右シフトすると、数値は2分の1となります。

桁あふれ(オーバーフロー)
コンピュータで数値を表現する場合、8ビットや16ビットなどあらかじめ表現範囲は決まっています。
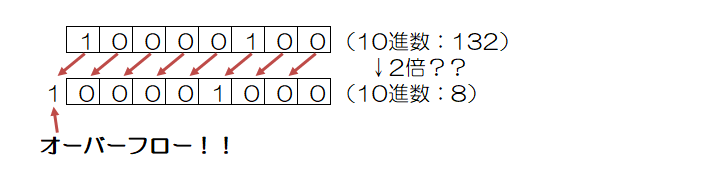
その為、シフトを行うと表現の幅を超え、ビットが飛び出してしまい、正確に数値が表現できない場合があります。これを「桁あふれ」または「オーバーフロー」といいます。
シフトの種類
シフト演算には、符号ビットを考慮しない「論理シフト」と、符号ビットを考慮してそのままにする「算術シフト」があります。
論理シフト
論理シフトでは、符号ビットを考慮しません。最上位のビットも含めてシフトを行います。
シフトすることによって飛び出したビットは捨てられ、空いたビットには0が入ります。
シフトによって飛び出したビットに1が入っていた場合、桁あふれが発生し、正しい計算結果を得ることが出来ません。
左にシフトして桁あふれが発生した場合を「オーバーフロー」、右にシフトして桁あふれが発生した場合を「アンダーフロー」といいます。
左論理シフト
左論理シフトでは、左にNビットシフトすると、左側の上位Nビットが飛び出して捨てられます。その分、右側の下位Nビットが空き、そこには0が入ります。
但し、シフトによって飛び出したビットに1が入っていた場合、オーバーフローが発生し、正しい計算結果を得ることが出来ません。
右論理シフト
右論理シフトでは、右にNビットシフトすると、右側の下位Nビットが飛び出して捨てられます。その分、左側の上位Nビットが空き、そこには0が入ります。
但し、シフトによって飛び出したビットに1が入っていた場合、アンダーフローが発生し、正しい計算結果を得ることが出来ません。

算術シフト
算術シフトでは符号ビットを考慮して、先頭の最上位ビットはそのまま移動しません。最上位以外のビットだけをシフトします。
負の数を2の補数で表現する、符号付きの2進数の場合は算術シフトが使われます。
左算術シフト
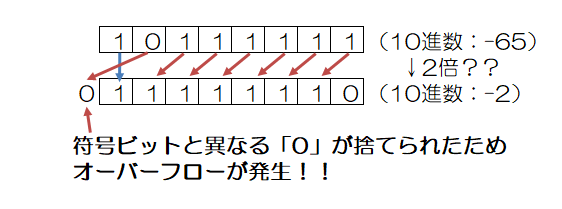
左算術シフトでは、先頭の符号ビットは移動せず、それ以外のビットを左にシフトします。先頭の符号ビットが移動しない以外は論理シフトと同様です。
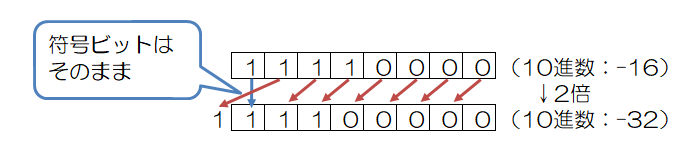
算術シフトの場合は、シフトによって飛び出したビットに「符号ビットと異なる値」が入っていた場合、オーバーフローが発生し、正しい計算結果を得ることが出来ません。
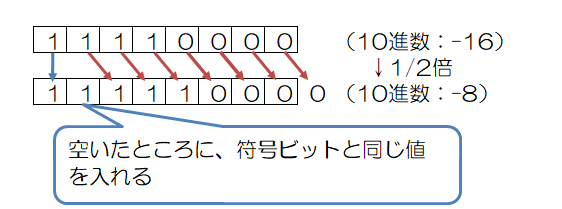
右算術シフト
右算術シフトでは、先頭のの符号ビットは移動せず、それ以外のビットを右にシフトします。
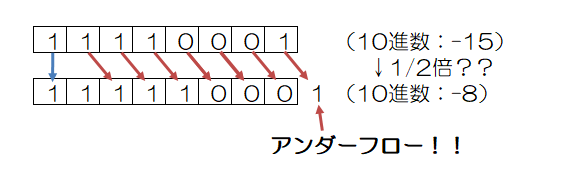
シフトによって左側に空いたビットには、符号ビットと同じ値が入ります。
但し、シフトによって飛び出したビットに1が入っていた場合、アンダーフローが発生し、正しい計算結果を得ることが出来ません。
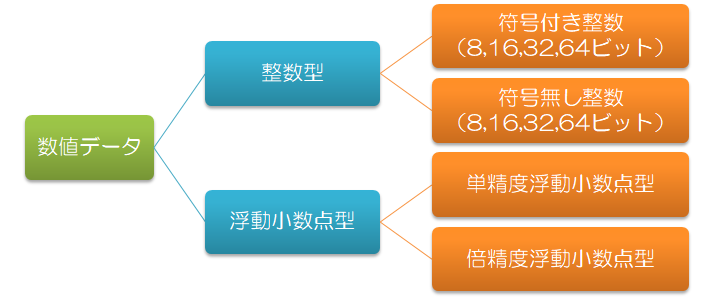
数値データの形式と誤差
コンピュータでは扱う情報に応じて、数値の表現方法が使用される。
使用する数値データの形式により、精度、扱える範囲、データサイズ、誤差の生じやすさが異なってくる。
誤差の種類
誤差の種類としては以下の様なものがある。
- オーバーフロー、アンダーフロー:扱えるデータの範囲を超えた時の誤差。
- 丸め誤差:無限小数の桁を区切った際に発生。
- 情報落ち:絶対値の大きい数と小さい数を加減算した時、絶対値の小さい値が無視される。
- 桁落ち:値がほぼ等しく、丸め誤差を持った数値同士の減算を行なった場合に有効数字が減少