この記事での学習内容 ITパスポート 基本情報 応用情報
木構造の種類と考え方、木の巡回法、節の追加や削除、ヒープの再構成などを理解する。
用語例:根、葉、枝、二分木、完全二分木、バランス木、順序木、多分木、探索木、深さ優先探索、幅優先探索、先行順、後行順、中間順
木構造
木構造はデータ間の階層的な関係、つまり親と子のような関係を表現するのに用いられるデータ構造です。大量の情報を系統的に管理する際に有効です。
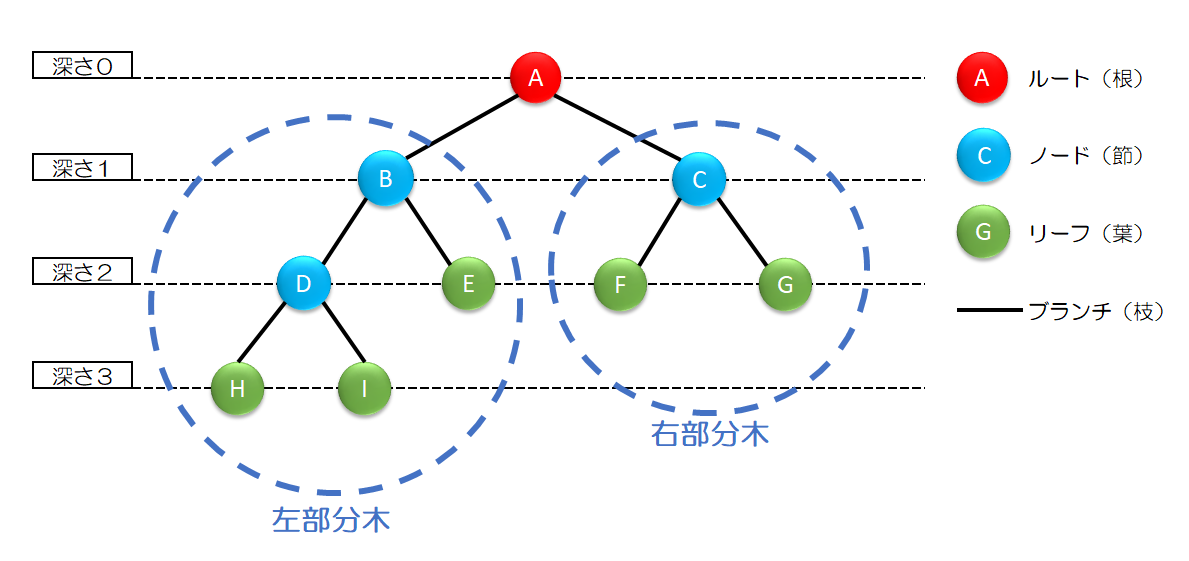
木構造は、「節(ノード)」と「枝(ブランチ)」から構成されています。最上位の節は「根(ルート)」といいます。また、最下位の節を「葉(リーフ)」といいます。複数に枝分かれしている場合には、「葉(リーフ)」は複数になります。「枝(ブランチ)」は節と節をつなぐ経路のことです。
また、ある節の上の枝につながる節を親、下の枝につながる節を子といいます。
木構造では、親の節から子の節をたどっていくことでデータを取り出すことができます。
木構造の深さ
木構造では、節や葉の階層を示すため「深さ」という数値が使われます。深さは根の階層を0として、下に行くと1ずつ増えていきます。
部分木
木構造の部分を示す時に「部分木」という言葉が使われます。
ある節に注目した時、その節の左の枝から下の木構造を「左部分木」、節の右の枝から下の木構造を「右部分木」といいます。
二分木と多分木
節から出る枝が2本以下である木を二分木といいます。対して、節から出る枝が2本より多い気を多分木といいます。
二分木では、節の左側に繋がる部分を左の子(左部分木)、右側に繋がる部分を右の子(右部分木)といいます。
二分木の中で、根から葉までの深さが全て同じものを「完全二分木」と呼びます。一般的な二分木は「葉の深さの差が1以内である」、「葉を除く全ての節が左部分木を持っている」という二つの条件を満たすものです。
同じ階層の節に順位があるものを順序木といいます。順序木では一つの節の下の節や葉は左側のほうが高い順位と見なされます。順序木ではデータの格納方法を工夫することにより、データの検索や大小関係での並び替えを効率的に行うことが出来ます。
木の巡回法
木構造からデータを探して読み出すことを「木の巡回」といいます。二分木の巡回法には幅優先探索と深さ優先探索があります。
木の幅優先探索
幅優先探索を行うと、最初に子のデータを読み出します。子のデータが検索したデータでない場合は、1階層目の節や葉のデータを左から右へと順番に読み出していきます。1階層目のデータが検索したデータでない場合は、次は2階層目と進んでいく、という方法です。
木の深さ優先探索
深さ優先探索は、左部分木を優先して、階層が下のデータを先に読み出す方法です。
葉以外の節のデータと、葉のデータを読み出す順番の違いにより、先行順探索、中間順探索、後行順探索の3種類があります。
先行順探索
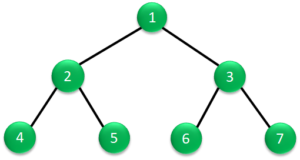
右の図を例にとって説明すると、最初の節である根のデータ1を読み出し、次に左部分木の節のデータ2を読み出します。
その次は2階層目の左部分木のデータ3を読み出します。
3階層目はないので、2階層目の右部分木のデータ4を読み出します。
中間順探索
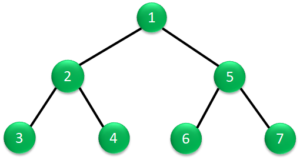
右の図を例にとって説明すると。根から始めて2階層目の左部分木で左部分旗がなくなるので、データ1を読み出します。
次に、上の階層に戻ってデータ2を読み出します。
その次に2階層目の右部分木のデータ3を読み出します。
2階層目の読み出しが終わると、次は根のデータ4を読み出します。
後行順探索
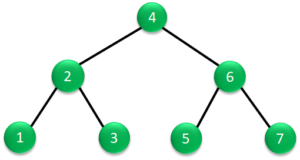
右の図を例にとって説明すると、根から始めて2階層目の左部分木で左部分旗がなくなるので、データ1を読み出します。
次は2階層目の右部分木のデータ2を読み出します。
その次は、上の階層に戻ってデータ3を読み出します。
その次は、1階層目の右部分木ですが、そこからは左部分木が出ているので、左部分木のデータ4を読み出します。
二分探索木の応用
二分木に対して、データを格納するルールを定めることにより、木構造をデータの検索や大小順での並び替えに活用できます。
データの検索に活用する例が「2分探索木」、整列に活用する例が「ヒープ」です。
2分探索木
二分木の中でも、左の木の全てのデータが親よりも小さく、右の木の全てのデータが親よりも大きいという声質を持つ木を「2分探索木」といいます。
なお、2分探索木は完全二分木である必要はありません。
データの探索
2分探索木を用いると、節毎に大小関係を比較することにより、データの探索を効率的に行うことが出来ます。
例えば、9階層の木構造の場合、深さ優先探索や幅優先探索を行うと、最大で1000回を越える比較が行われますが、2分探索木ならば、比較回数は10回未満で済みます。
データの追加
2分探索木にデータを追加する場合は、検索と同じような手順で、追加する場所を探していきます。
データを追加した後も2分探索木になるようにします。
データの削除
2分探索木でデータを削除する場合、削除する節の持つ枝の数により処理が異なります。
- 枝のない葉の場合: そのまま葉を削除します。
- 枝が1本の場合: 節を削除して、下の節をつなぎ直します。
- 枝が2本の場合: 削除する節の左部分木の中で、最も大きな値のデータを削除する節に移動します。
削除をこの手順で行うことにより、削除を行った後も2分探索木になるようにします。
バランス木
木構造は、追加や削除を繰り返していくうちに、葉の深さにばらつきが出て、部分木のバランスが悪くなることがあります。
部分木のバランスが悪くなると、探索の効率が低下してしまうので、一定のルールを定めて、部分木のバランスを取る木構造があります。そのような木構造を「バランス木」といいます。
完全二分木はバランス木の一種です。他のバランス木には「AVL木」や「B木」があります。
AVL木
葉の深さの差が常に1以下の木構造です。完全二分木と異なり、葉でない節が左部分木を持つ必要はありません。
AVL木では、要素の追加や削除が発生する時に、バランスが崩れていないかをチェックしつつ、崩れていればそれを回復する処理(=再構築)を行う必要があります。そのため、追加や削除が発生する場合には、通常の2分探索木より手間がかかるのですが、バランスを取りながら木の深さを浅く保つことで、探索時のコストを抑えることが可能になります。
B木
B木は多分木のバランス木の一つです。一つの節に入れられるデータの個数や分岐の数は、「次数」と呼ばれる数値で決まります。
次数をNとするB木を「N次のB木」といいます。N次のB木は以下の4つの条件を満たす必要があります。
- 一つの節のデータ数は2×N個以下であること。
- 根以外の節はN個以上のデータを持つこと。
- 葉以外の節はデータ数+1個の枝を持つこと。
- すべての葉は同じ階層であること。
バランス木の実用例
バランス木の実用例としては、データベースの「インデックス(索引)機能」にB木が多く利用されています。(AVL木を使う場合もあります。)
検索の処理を高速に行うことを優先したい場合には、単純な2分探索木よりも、バランス木が用いられます。
単純な2分探索木で最初の木構造の作り方が悪いと、偏った木構造となり、検索のコストがリスト構造と変わらなくなることがあるためです。