この記事での学習内容 基本情報 応用情報

形式言語とは何か、言語の定義、演算、種類、文法を理解する。また、BNF、構文図式などの表記法、正規表現、文脈自由文法を理解する。

用語例： 逆ポーランド表記法

自然言語と形式言語

日本語や英語などの言語は人間が暮らしていく中で自然に発生したため、必ずしも厳密な文法に従っているとは限りません。こういった言語を自然言語といいます。

それに対し、特定の目的のために作られ、厳格な文法に則った言語を形式言語といいます。
コンピュータに指示を与えるためには、プログラミング言語と呼ばれる言語を用いたプログラムを作成します。
このプログラミング言語も形式言語の一つです。

文脈自由文法

言語に関するルールを定めたものが『文法』で、制限の強さの異なる4つの分類があります。ここでいう文法は文の形式を定めるだけで意味についての解釈は行いません。

• 句構造文法
• 文脈依存文法
• 文脈自由文法
• 正規文法

句構造文法が制限が最も弱く、正規文法が最も制限が強い文法です。形式言語では、文脈自由文法が用いられます。

文脈自由文法は、プログラミング言語を正確に記述するための厳密な形式を定めることが出来る文法です。

例えば、文脈自由文法で『直角とは90度である』と定義する場合、定義が必要なもの（この場合は「直角」）を「非終端記号」といい、それ以上他のものに置き換えることが出来ずに定義が必要でないもの（この場合は「90度」）を「終端記号」といいます。

BNF記法（バッカス・ナウア記法）

BNF（Backus-Naur Form）は、文脈自由文法の文法自体を定義するための記法で、一般的には、バッカス・ナウア記法と呼びます。
プログラミング言語 algol60の文法定義に初めて用いられた記法です。

記号	意味
＜変数名＞	＜非終端記号＞（＝メタ変数名）
::=	左辺が右辺に分解できることを表す。（○○とは▲▲であるの部分を表す）
｜	「または」を表す

現在では、ヴィルド博士がBNFを拡張して作成したEBNF（拡張バッカス・ナウア記法）も一般的です。
BNFとEBNFの相違は、EBNFでは繰り返し部分を中かっこで囲んだり、終端記号をダブルクォーテーションやシングルクォーテーションで囲んだり、といった違いがあります。

例：

• <a> ::= <b>　　aはbである。
• <a> ::= 1｜2　　aは1または2である。

例2（数値の表現をBNF記法で表した例）

• ＜数値＞::= ＜数字列＞｜＜符号＞＜数字列＞｜＜数字列＞.＜数字列＞
• ＜数字列＞::=＜数字＞｜＜数字列＞＜数字＞
• ＜数字＞::=0｜1｜2｜3｜4｜5｜6｜7｜8｜9
• ＜符号＞::= +｜-

この例の＜数字列＞の定義のように、自身の定義の中で自らを定義するような書き方が、情報処理の分野ではよく用いられます。このような定義の仕方を「再帰（的）」と呼びます。

構文図式

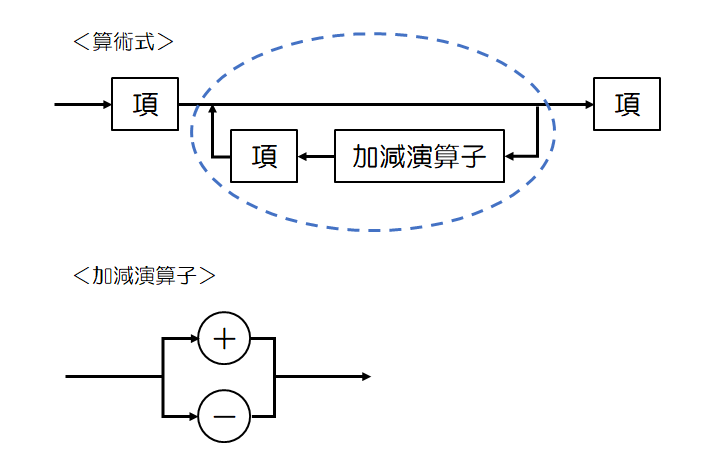
構文図式は、BNFで定義した文法の構造、「構文」を視覚的に表現する方法の一つです。

以下に、BNFのと構文図式の例を示します。

＜算術式＞のBNF表記

• ＜算術式＞::=＜項＞｜＜加減演算子＞＜項＞
• ＜加減演算子＞::= ＋｜－

なお、点線で囲っている部分は0回以上の繰り返しを表します。

正規表現

正規表現とは、いくつかの文字をパターン化して一つの形式で表現する表記法です。BNFを記述するときにも使われます。

正規表現を用いることで、個別の文字列を指定しなくても、また表記にゆれがあっても検索することが可能です。

例えば、以下のようなケースで正規表現を用いて、文字列を検索します。

• 数値のみで構成されている任意の文字列を検索したい
• 「ユーザ」と「ユーザー」といった、調音の有無を無視して検索したい

例）メールアドレスの表記ルールを正規表現で表す

正規表現：　[\w\d_-]+@[\w\d_-]+\.[\w\d\._-]+

正規表現で用いられる記号の例

• \w　半角英字（a～z、A～Z）
• \d　半角数字（0～9）
• \.　半角ピリオド
• _　半角アンダースコア
• -　半角ハイフン
• [\w\d_-]　［］内のいずれか1文字
• +　直前の正規表現の1回以上の繰り返し
• .　任意の1文字
• *　直前の正規表現の0回以上の繰り返し

逆ポーランド記法

演算方法の表記法の一つに「逆ポーランド記法（Reverse Polish Notation : RPN）」があります。
数式を記述する際、演算子を演算対象の後ろに置く方法です。

逆ポーランド記法はコンピュータと相性の良い数式の書き方です。なぜなら、コンピュータは人間と違って与えられた情報を俯瞰的に眺めることは苦手であり、基本的には「右から来た情報を左に受け流す」というのがコンピュータの情報の扱い方なので、逆ポーランド記法のように、情報を流れてきた順序に沿って処理できる方法と相性が良いからです。
また、コンピュータが持つ「スタック」というデータの管理機構で数式を処理しやすい、という面もあります。

スタックは「積み重ねる」という意味で、最後に入れたものを最初に取り出すデータ構造です。

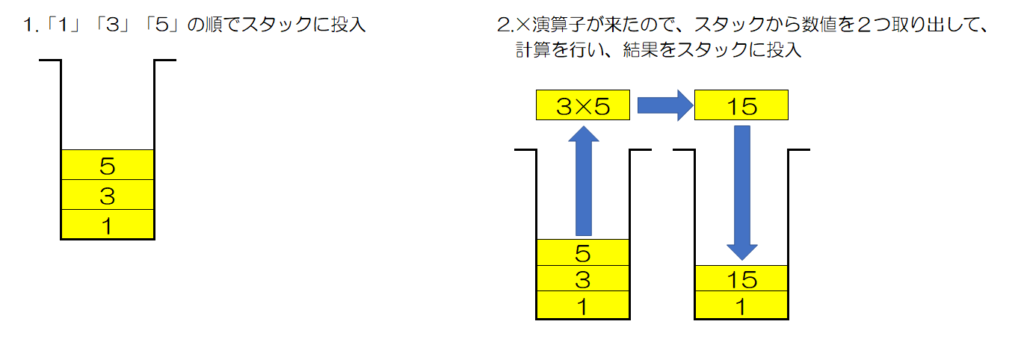
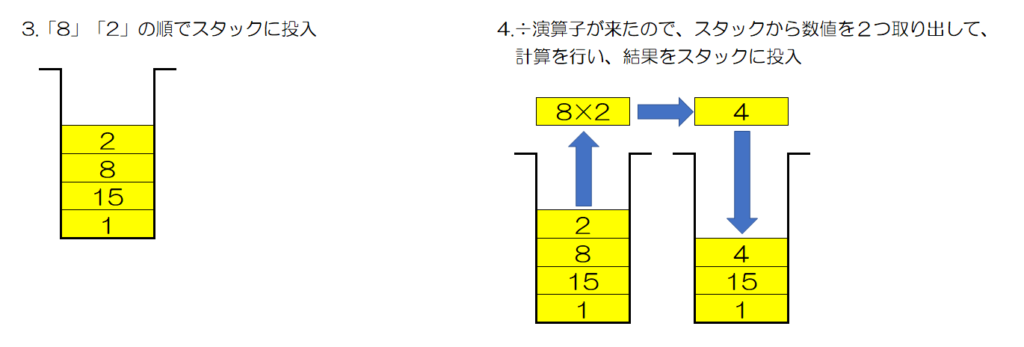
実際に、逆ポーランド記法で書かれた、「135×82÷++」という計算式を、スタックを用いて計算してみましょう。
基本的な動作は、以下の2つです。

• 数値が来たら、スタックに投入する。
• + や – などの演算子が来たら、スタックから数値を2個取り出して計算し、その結果をスタックに投入する。